数独-超難問集3/10-解答

数独-超難問集の3/10問目

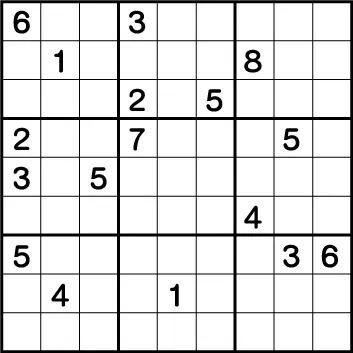
下記の解答を見る前に是非ノーヒントで数独難問にチャレンジしてみてください。
下記のリンクから、PDFをダウンロード・印刷することが可能です。
PDF-数独-超難問集3/10をダウンロード・印刷

アナログではなくデジタルでチャレンジしたい方は、少し手間ですが、下記のリンク先にて問題を入力することでデジタルで数独難問にチャレンジすることが可能です。数独を楽しむことはもちろん、簡単な手順も解析もしてくれるので、参考にしてみても良いかと思います。※背理法等のトライアンドエラーで進める手順は解析されないので注意が必要です。

説明を始める前に、わかりやすいように各所の呼び名を決めておきたいと思います。

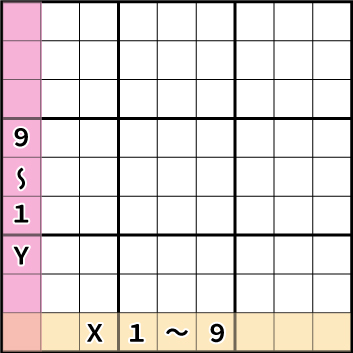左下を基準に行（横）をX1～9、
そして、列（縦）をY1～9とします。

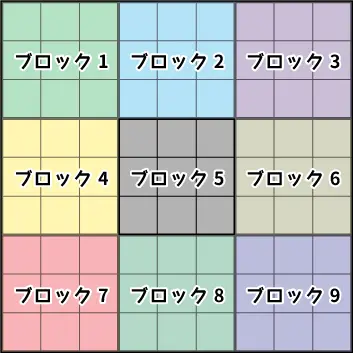次に左上を基準に3×3マスの9マスをブロック1～9とし説明していきたいと思います。ここで紹介している数独は上級者向けの難問となっています。「数独って？」「数独のルールは？」という方は下記の記事を参考にしてみてください。数独の基本ルールを紹介しています。

数独-難問手順.1-ブロック2の《1》を確定させます。

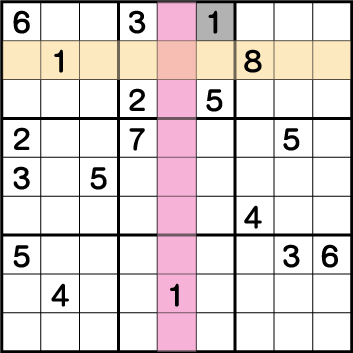ブロック1とブロック8に配置している《1》からブロック2の《X:6 Y9》が《1》であることがわかります。

数独-難問手順.2-ブロック4の《4》を確定させます。

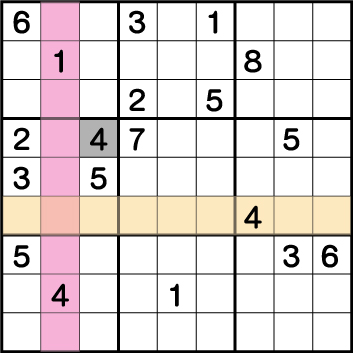ブロック6とブロック7に配置されている《4》からブロック4の《X:3 Y:6》が《4》であることがわかります。

数独-難問手順.3-ブロック1とブロック3の《5》を確定させます。

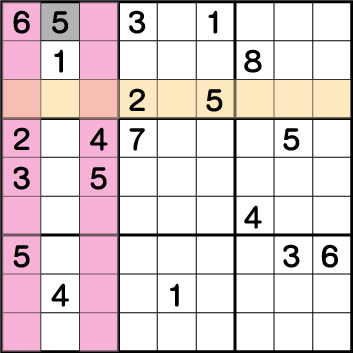ブロック2・4・7に配置されている《5》からブロック1の《X:2 Y:9》に《5》が入ることが分かります。次いで・・・・

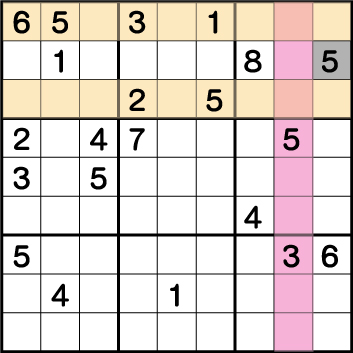ブロック1の《5》が決定したことで、ブロック3の《X:9 Y8》にも《5》が入ることがわかります。

数独-難問手順.4-ブロック1・7・8の《3》を確定させます。

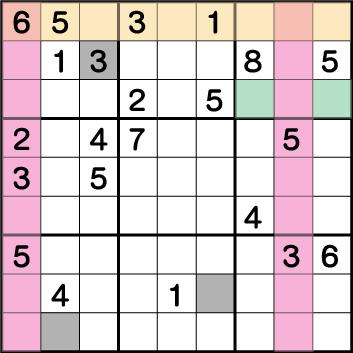まず、ブロック1の《3》についてですが、ブロック2と9に配置されている《3》からグリーン部分の《X:7/9 Y7》のいずれかに《3》が入ることがわかります。結果、《X:2/3 Y:7》から《3》が候補と消え、《X:3 Y:8》に3が入ることがわかります。

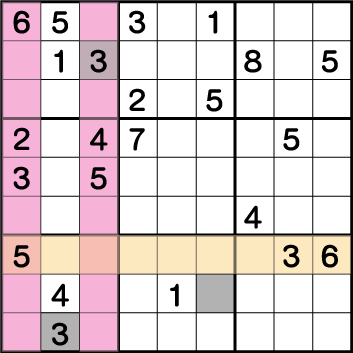ブロック1の《3》が確定したら、ブロック7の《3》が確定し・・・

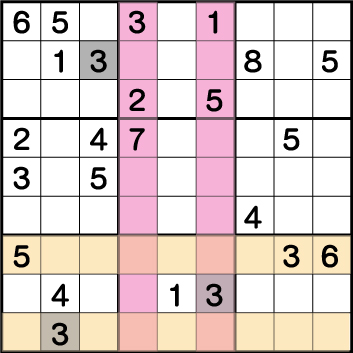ブロック7の《3》が確定したら、ブロック8の《3》が確定します。

数独-難問手順.5-ブロック5の《1》を確定させます。

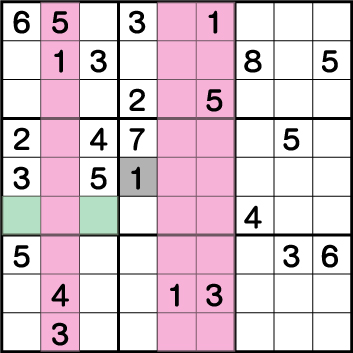ブロック1に配置されている《1》からブロック4のグリーン部分に《1》が入ることがわかり、《X:4 Y:4》に《1》が入らないことがわかります。結果候補として残っている《X:4 Y:5》に《1》が入ることがわかります。

数独-難問手順.6-ブロック1・7・3の《2》を確定させます。

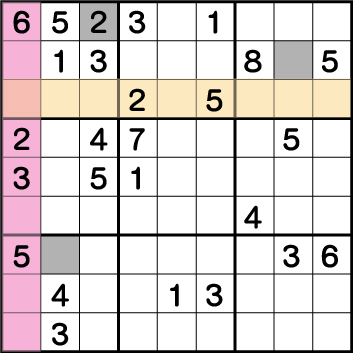まず、ブロック1は、ブロック2そしてブロック4の《2》の配置により《X:3 Y:9》に《2》が入ることがわかります。

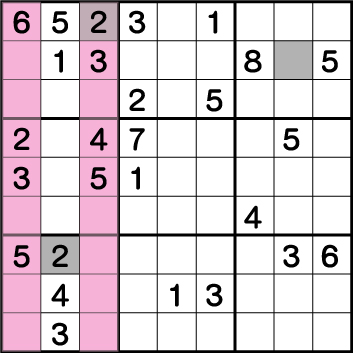ブロック1の《2》が確定するとブロック7の《2》も確定します。

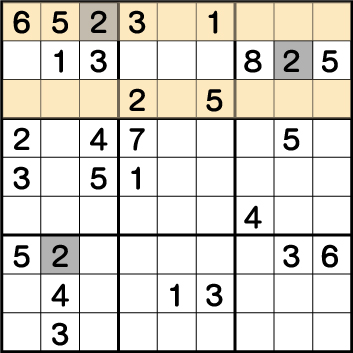同様に、ブロック3の《2》も確定します。

数独-難問手順.7-ブロック2の《8》を確定させます。

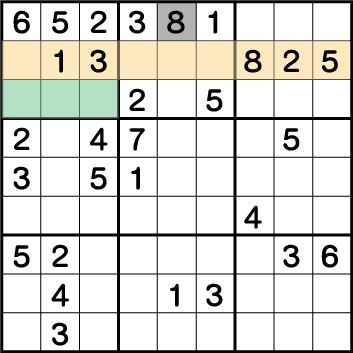ブロック3に配置されている《8》により、ブロック1には《X:1/2/3 Y:7》のいずれかに《8》が入ることが確定するため、《X:5 Y:7》のマスから候補として《8》が除外されます。結果、《X:5 Y:9》に《8》が入ることがわかります。

数独-難問手順.8-背理法を使用して、《X:8 Y:7》を確定させます。

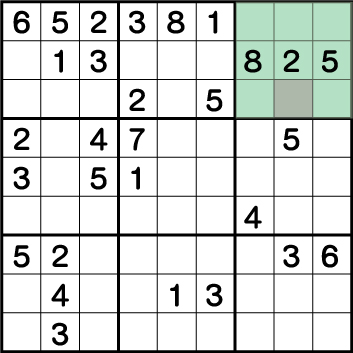まだ、中盤前ですが通常テクニックではすでに手詰まり状態となってしまっています。ということで背理法を使用して手を進めていきます。今回ターゲットとするマスは《X:8 Y:7》となります。まずは、《X:8 Y:7》に入る候補を洗い出します。

行《Y:9》からブロック3の上段3マスは、《4・7・9》が入る専用マスとなっています。このことから下段の3マスは《1・3・6》の専用マスになっていることがわかります。

さらに、ブロック9の《3》の配置から 《X:8 Y:7》には《1もしくは6》が入るマスであることがわかります。《1》と《6》どちらかかが正解でどちらかが誤りとなるので、とりあえず数字を入れて見て矛盾点が無い方が正解となります。

まず最初に《1》を入れて手を進めて見ます。すると以下のような結果になりました。

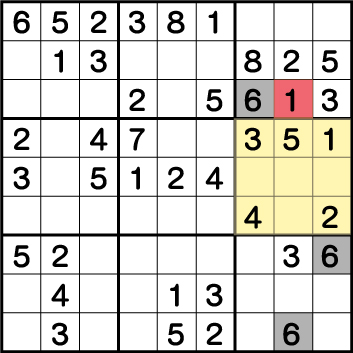ブロック6に《6》を入れることができなくなってしまいました。つまり、《X:8 Y:7》の候補として《1》が除外され、残った《6》が正解となります。

ちなみに、背理法を使用するマスを選ぶ際のポイントは候補となる数字が少なく、かつそのマスが確定することで手が進みそうなマスを選択するところにあります。背理法は理論的にどのマスでも使用可能ですが候補の数字が5つも6つもある場合は時間ばかりかかってしまい疲れるだけですので・・・

数独-難問手順.9-ブロック3の《4》そしてブロック9の《1》を確定させます。

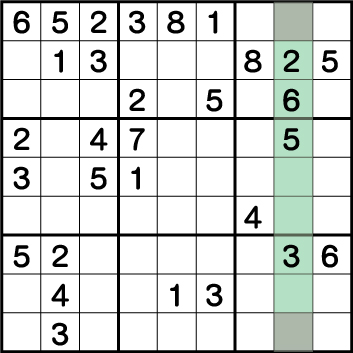まず、列《X:8》の空きマスに入る候補を、各空きマスのブロック・列・行から全て洗い出します。上から順に・・・

《X:8 Y:9》＝《4・7・9》
《X:8 Y:5》＝《7・8・9》
《X:8 Y:4》＝《7・8・9》
《X:8 Y:2》＝《7・8・9》
《X:8 Y:1》＝《1・4・7・8・9》

となります。《X:8 Y:4》に候補として《1》が入りそうな気もしますが、ブロック4の《X:1/3 Y:4》のいずれかに《1》が入ることが確定しているので、《X:8 Y:4》から候補として《1》が除外されます。

少し脱線しましたが、ここで注目したいのが、《X:8 Y:2/4/5》の3マスです。これらのマスには前述の通り《7・8・9》のいずれかがはいることが確定しています。逆に言うと、これらの3マスは《7・8・9》の専用マスになるわけです。その結果・・・・

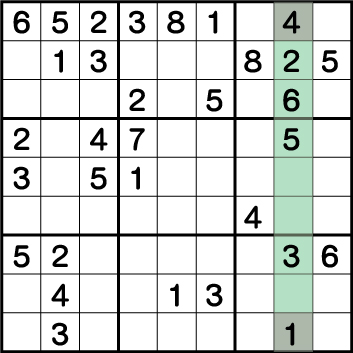《X:8 Y:9》＝《4・7・9》から《7・9》が除外され《4》が確定され、さらに《X:8 Y:1》＝《1・4・7・8・9》から《4そして7・8・9》が除外され《1》が確定します。

数独-難問手順.10-ブロック7・ブロック4の《1》を確定させる。

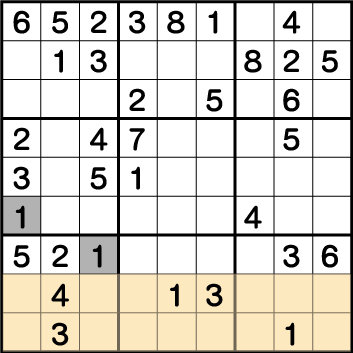ブロック9の《1》が確定したことにより、ブロック7の《1》を。そしてブロック4の《1》を確定させることができます。

数独-難問手順.11-ブロック9の《4》を確定させます。

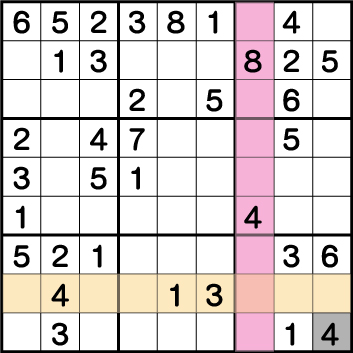ブロック6・ブロック7の《4》の配置からブロック9の《4》が確定します。

数独-難問手順.12-ブロック9の《5と2》を確定させます。

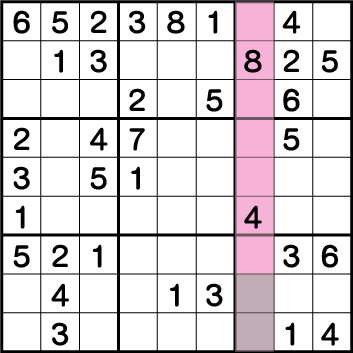手順9の時ど同様に列《X:7》に入る空きマスの全ての候補をブロック・列・行から全て洗い出します。上から順位チェックしてきます。

《X:7 Y:9》＝《7・9》
《X:7 Y:7》＝《1・3》
《X:7 Y:6》＝《1・3・6・9》
《X:7 Y:5》＝《2・6・7・9》
《X:7 Y:3》＝《7・9》
《X:7 Y:2》＝《2・5・7》
《X:7 Y:1》＝《5・7・9》

《X:7 Y:1》の候補として《2》も考えられそうですが、ブロック2そしてブロック7の《2》の配置により《X:5/6 Y:1》のいずれかに《2》が入ることが確定しているため、《X:7 Y:1》の候補から《2》は除外されます。

上記のリストから《X:7 Y:3/9》が《7・9》の専用マスであることが確定されるため、他のマスから《7・9》を除外します。すると・・・

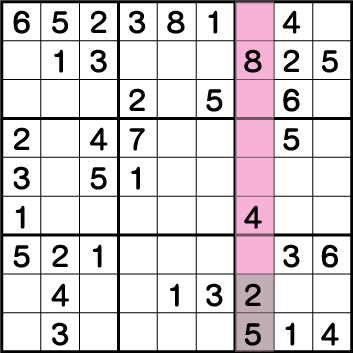《X:7 Y:9》＝《7・9》
《X:7 Y:7》＝《1・3》
《X:7 Y:6》＝《1・3・6》
《X:7 Y:5》＝《2・6》
《X:7 Y:3》＝《7・9》
《X:7 Y:2》＝《2・5》
《X:7 Y:1》＝《5》

となり、《X:7 Y:1》＝《5》が決定したことにより、《X:7 Y:2》＝《2》ということも決定します。さらに、《X:7 Y:5》＝《6》といことも確定します。

数独-難問手順.13-ブロック8・ブロック5の《5》を確定させる

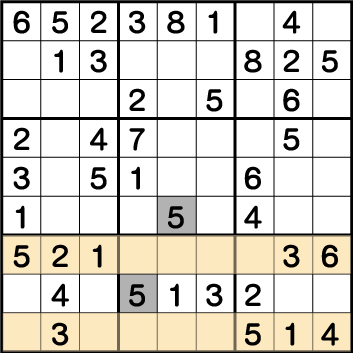ブロック9の《5》が確定したことにより、ブロック8の《5》が確定し、次いで、ブロック5の《5》が確定します。

数独-難問手順.14-ブロック7の《6》を確定させます。

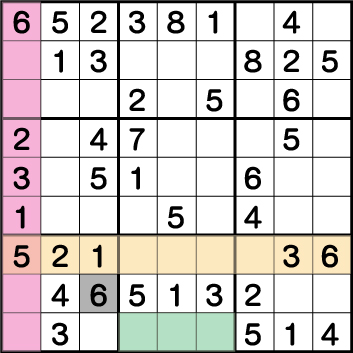ブロック1そしてブロック9の《6》の配置により、ブロック7には《X:3 Y1/2》のいずれかに《6》が入ることがわかります。そしてブロック8にはグリーンのエリアのいずれかに《6》が入ることから《X:3 Y:1》に《6》が入る可能性が消え、結果《X:3 Y:2》に《6》が入ることが分かります。

数独-難問手順.15-ブロック5の《3》⇒ブロック6の《1》⇒ブロック3の《3・1》を確定させます。

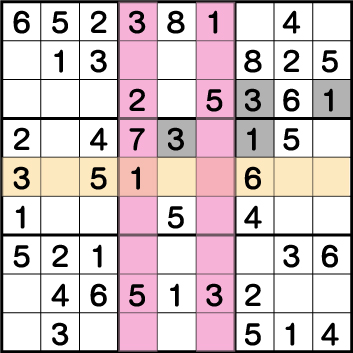ブロック2、ブロック4そしてブロック8の《3》の配置からブロック5の《3》が確定します。

前述までにすでに《X:7 Y:6》《X:7 Y:7》《X:9 Y:7》の候補は《1・3》のみとわかっていたので、残りのグレーマスの《1と3》が確定します。

数独-難問手順.16-ブロック6の《3と2》を確定させます。

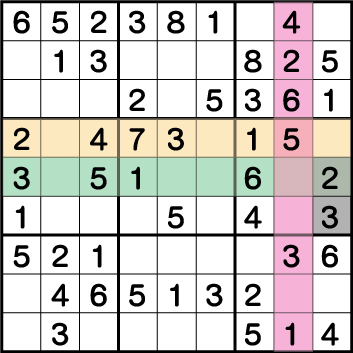ブロック5の《3》が確定したことにより、ブロック6の《3》も確定。ついで、《2》も確定し・・・

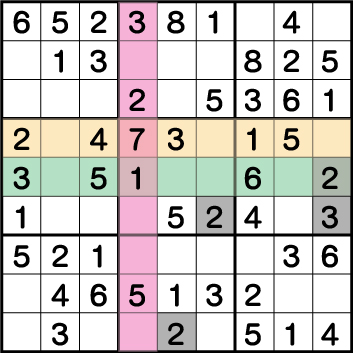そのまま、ブロック5、そしてブロック8の《2》も確定します。

数独-難問手順.17-ブロック2の《6》を確定させます。

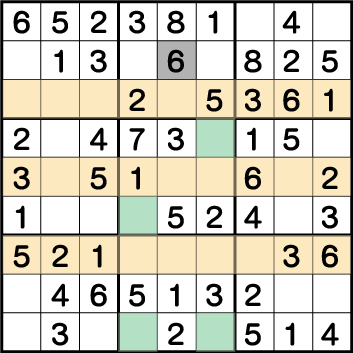ブロック5、そしてブロック8に《6》が入る候補のマスはグリーンエリアの4か所のうち2か所です。どこの候補に入っても、同列であるブロック2の《X:4/6 Y:8》に《6》を入れることができません。結果、《X:5 Y:8》に《6》が入ることになります。

数独-難問手順.18-背理法で《X:7 Y:9》を確定させます。

手順18で手詰まりとなってしまったので、背理法を使用して手を進めていきます。繰り返しになりますが、背理法は手が進みそうな箇所を予想して矛盾点を洗い出す手法となります。

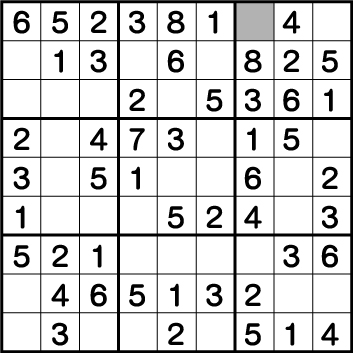数独難問も終盤になるので、いろいろな箇所で背理法が有効ですが、今回は、《X:7 Y:9》にあたりをつけて矛盾点を探ってみます。候補は《7》もしくは《9》です。とりあえず《9》を入れて手を進めています。

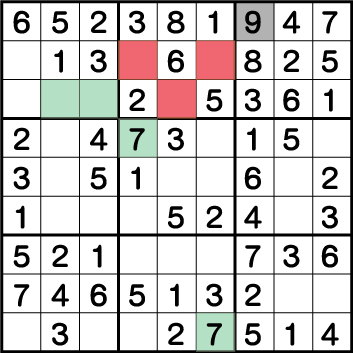するとこのように矛盾が発生してしまいました。グリーンのエリアには7が入る箇所になるのですが、その結果ブロック2に《7》を入れることができなくなっています。つまり《X:7 Y:9》に入る数字は、《7》ということがわかります。

数独-難問手順.19-最終回答

背理法でブロック3の《7》を確定させることができれば、後は芋づる式で他のマスを埋めることが可能です。

まとめ-数独-超難問集3/10-解答

今回の数独難問は背理法を2回も必要とするかなり難易度が高いものとなりました。背理法以外にも複数数字の専用マスについての理解もないと解けない問題となっています。