
数独-超難問集の1/10問目。背理法を必要とする難易度の非常に高い問題
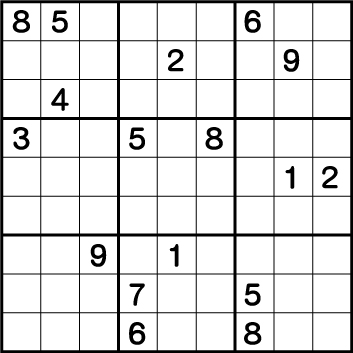
下記の解答を見る前に是非ノーヒントで数独難問にチャレンジしてみてください。
下記のリンクから、PDFをダウンロード・印刷することが可能です。
PDF-数独-超難問集1/10をダウンロード・印刷
アナログではなくデジタルでチャレンジしたい方は、少し手間ですが、下記のリンク先にて問題を入力することでデジタルで数独難問にチャレンジすることが可能です。数独を楽しむことはもちろん、簡単な手順も解析もしてくれるので、参考にしてみても良いかと思います。※背理法等のトライアンドエラーで進める手順は解析されないので注意が必要です。
ナンプレを解析。基本戦術で進めることができるナンプレの手順を解説。
説明を始める前に、わかりやすいように各所の呼び名を決めておきたいと思います。
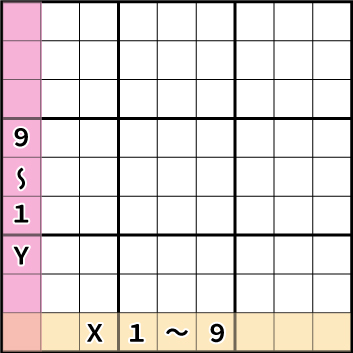 左下を基準に行(横)をX1~9、
左下を基準に行(横)をX1~9、
そして、列(縦)をY1~9とします。
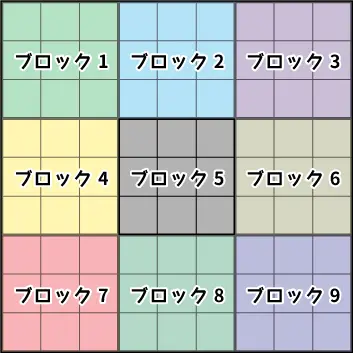 次に左上を基準に3×3マスの9マスをブロック1~9とし説明していきたいと思います。ここで紹介している数独は上級者向けの難問となっています。「数独って?」「数独のルールは?」という方は下記の記事を参考にしてみてください。数独の基本ルールを紹介しています。
次に左上を基準に3×3マスの9マスをブロック1~9とし説明していきたいと思います。ここで紹介している数独は上級者向けの難問となっています。「数独って?」「数独のルールは?」という方は下記の記事を参考にしてみてください。数独の基本ルールを紹介しています。
ルールは、《列》《行》《ブロック》に1~9の数字を入れるだけです。ただし、同エリアに同じ数字が入ってはいけません。小学生でもわかる簡単なルールですが、大人でも苦戦するペンシルパズルそれが数独(別名:ナンプレ)です。 数独 …
数独-難問手順.1-初期配置からわかる、《X:1 Y7》を埋める
まず初期配置から、ブロック1に9が入るマスは1か所しかありません。
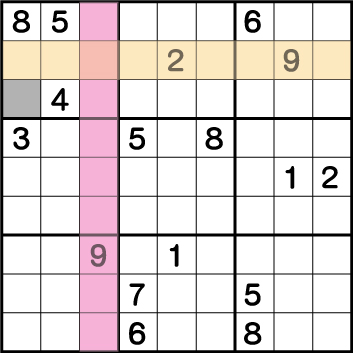 《X:1 Y7》が9であることが確定しています。
《X:1 Y7》が9であることが確定しています。
数独-難問手順.2-ブロック4の《1》と《2》を確定させます。
次にブロック4の《1》と《2》を埋めます。その為には、まずブロック6にある《1》《2》に注目します。
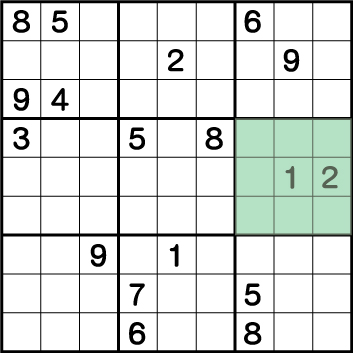 ここからブロック4そしてブロック5に入る《1》と《2》が入るマスの候補を探していきます。分かりやすいようにラインを引いてみます。
ここからブロック4そしてブロック5に入る《1》と《2》が入るマスの候補を探していきます。分かりやすいようにラインを引いてみます。
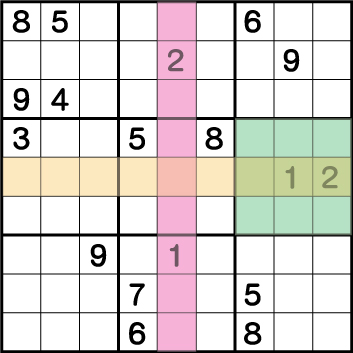 ラインを引いているマスには《1・2》を入れることができません。つまり《X:4/6 Y:4》は《1・2》の専用マスとなり、それ以外の数字を入れることはできません。
ラインを引いているマスには《1・2》を入れることができません。つまり《X:4/6 Y:4》は《1・2》の専用マスとなり、それ以外の数字を入れることはできません。
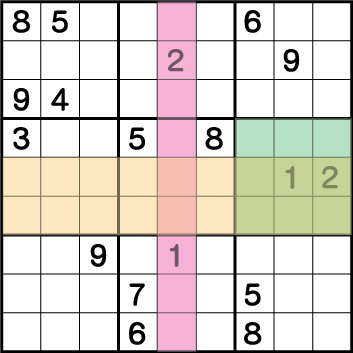 このことから、《X:2/3 Y:6》の2マスは《1・2》の専用マスであることが確定します。次に、ブロック2中央に配置されている《2》に注目してみます。
このことから、《X:2/3 Y:6》の2マスは《1・2》の専用マスであることが確定します。次に、ブロック2中央に配置されている《2》に注目してみます。
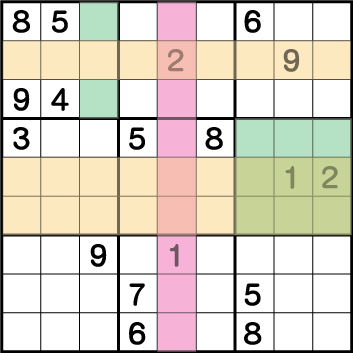 すると、ブロック1に入る《2》の候補は緑表示の《X:3 Y:7/9》の2マスのいずれかとなります。このことから同じ列にあたる、《X:3 Y:6》のマスの候補から2が消え《1》が確定し、次にその隣の《X:2 Y:6》のマスが2と確定します。
すると、ブロック1に入る《2》の候補は緑表示の《X:3 Y:7/9》の2マスのいずれかとなります。このことから同じ列にあたる、《X:3 Y:6》のマスの候補から2が消え《1》が確定し、次にその隣の《X:2 Y:6》のマスが2と確定します。
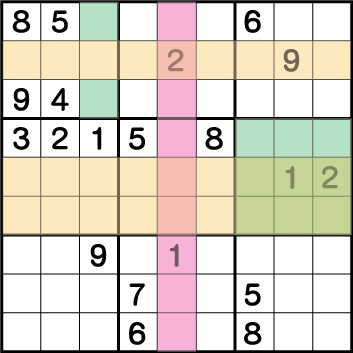
数独-難問手順.3-ブロック3の《1》、ブロック9の《2》を確定させます。
次はブロック3、ブロック9のグレー部分の数字を確定させていきます。まずは、ブロック3から見ていきます。ポイントは《1》となります。
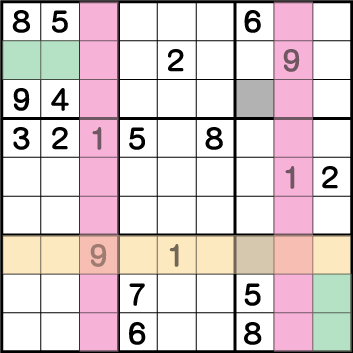 《1》が入るラインにピンク・オレンジの色を付けています。これにより、ブロック1には《X:1/2 Y:8》のいずれか、そしてブロック9には《X:9 Y:1/2》のいずれかに《1》が入ることが確定しました。つまり・・・
《1》が入るラインにピンク・オレンジの色を付けています。これにより、ブロック1には《X:1/2 Y:8》のいずれか、そしてブロック9には《X:9 Y:1/2》のいずれかに《1》が入ることが確定しました。つまり・・・
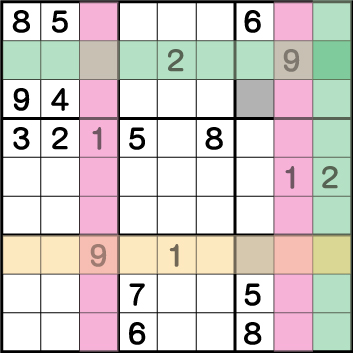 ピンク・オレンジ・ミドリのライン上には《1》が使用できないことが確定します。結果残った1マス《X:7 Y:7》に《1》が入ることがわかります。次に、ブロック9の《X:7 Y:3》についてですが、今度は《2》に注目します。
ピンク・オレンジ・ミドリのライン上には《1》が使用できないことが確定します。結果残った1マス《X:7 Y:7》に《1》が入ることがわかります。次に、ブロック9の《X:7 Y:3》についてですが、今度は《2》に注目します。
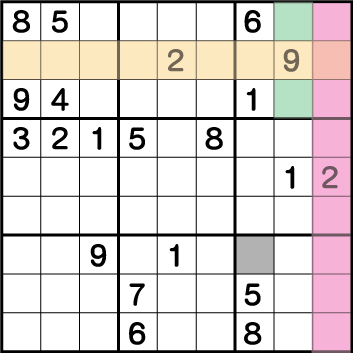 現在、配置されている《2》のライン上に色を付けると、《X:8 Y:7/9》のいずれかに2が入ることが分かります。
現在、配置されている《2》のライン上に色を付けると、《X:8 Y:7/9》のいずれかに2が入ることが分かります。
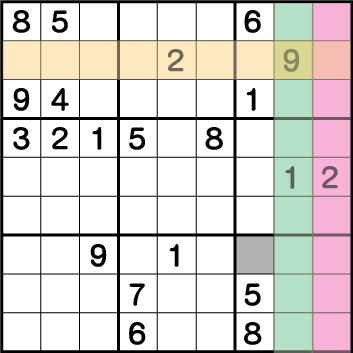 つまり、《2》を使用できない場所にラインを引くとこのようになり、残った《X:7 Y:3》に《2》が入ることが分かります。
つまり、《2》を使用できない場所にラインを引くとこのようになり、残った《X:7 Y:3》に《2》が入ることが分かります。
数独-難問手順.4-ブロック4の《1・2》を確定させます。
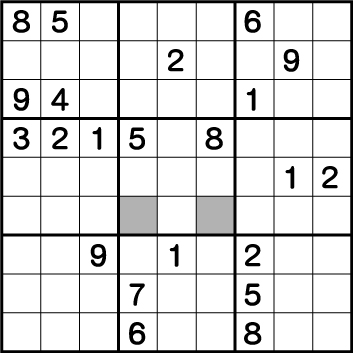
グレー部分の《X:4/6 Y4》は《1もしくは2》が入る専用マスであることは既に確定しています。
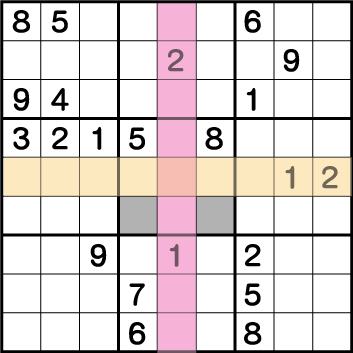 縦ライン・横ライン共に《1と2》が使用されているため、グレー部分の2マスは《1・2》専用であることはすぐにわかると思います。次に《2》だけに注目してブロック8をチェックしてみます。
縦ライン・横ライン共に《1と2》が使用されているため、グレー部分の2マスは《1・2》専用であることはすぐにわかると思います。次に《2》だけに注目してブロック8をチェックしてみます。
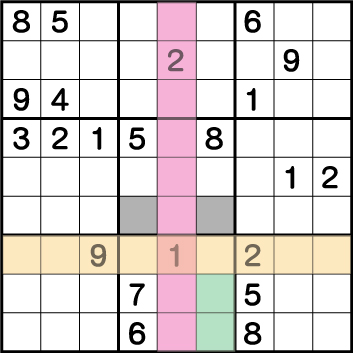 すると、《X:6 Y:1/2》のいずれかに必ず2が入ることがわかり、すぐ上に位置する《X:6 Y:4》に入る候補から《2》が除外されます。結果《X:6 Y:4》に《1》が。そして《X:4 Y:4》に《2》入ることがわかります。
すると、《X:6 Y:1/2》のいずれかに必ず2が入ることがわかり、すぐ上に位置する《X:6 Y:4》に入る候補から《2》が除外されます。結果《X:6 Y:4》に《1》が。そして《X:4 Y:4》に《2》入ることがわかります。
数独-難問手順.5-ブロック2の《1》を確定させます。
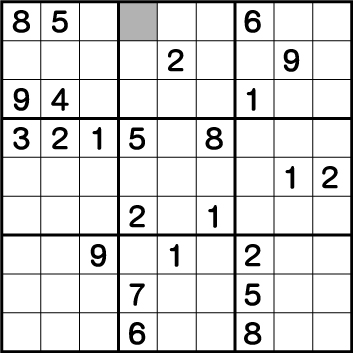
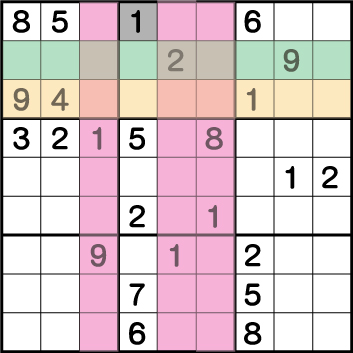 ブロック4にある《1》に注目すると、《X:1/2 Y:8》の2マスのいずれかに確定で《1》が入ることがわかり、《Y:8》の行に《1》を入れることができないことが分かります。
ブロック4にある《1》に注目すると、《X:1/2 Y:8》の2マスのいずれかに確定で《1》が入ることがわかり、《Y:8》の行に《1》を入れることができないことが分かります。
他に配置されている《1》を確認すると、《X:4 Y:9》が《1》で確定していることがわかります。
数独-難問手順.6-ブロック4/5/6の《9》を確定させます。

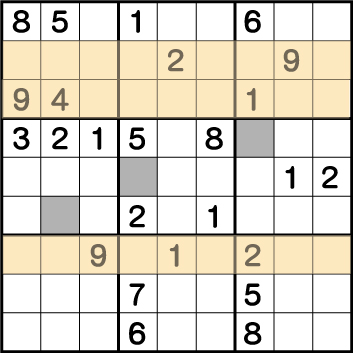 分かりやすいように、ポイントとなる部分の《9》にラインを入れて見ます。
分かりやすいように、ポイントとなる部分の《9》にラインを入れて見ます。
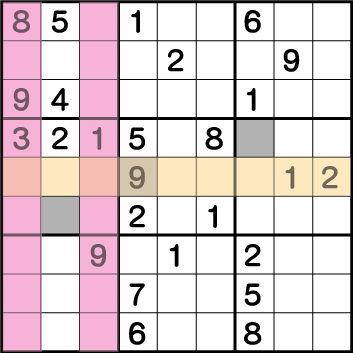 すると、《X:4》の列に空きマスが一つとなり、ブロック5の《9》が確定します。ブロック5の《9》が確定すると、ブロック4の《9》が確定します。3つめのブロック6についてですが・・・
すると、《X:4》の列に空きマスが一つとなり、ブロック5の《9》が確定します。ブロック5の《9》が確定すると、ブロック4の《9》が確定します。3つめのブロック6についてですが・・・
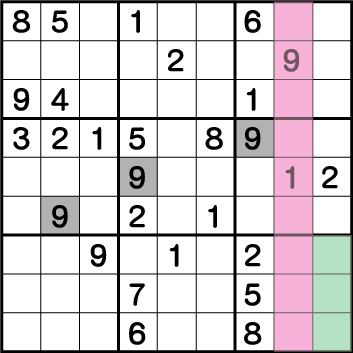 ブロック3の《9》により、グリーン部分の《X:9 Y1/2/3》のいずれかに《9》が入ることが確定しているため、ブロック6の《9》は必ず《X:7 Y4/5/6》のいずれかに入ることが確定しています。先ほどまでにブロック4・5の《9》が確定しているため、ブロック6の《9》は《X:7 Y:6》であることがわかります。
ブロック3の《9》により、グリーン部分の《X:9 Y1/2/3》のいずれかに《9》が入ることが確定しているため、ブロック6の《9》は必ず《X:7 Y4/5/6》のいずれかに入ることが確定しています。先ほどまでにブロック4・5の《9》が確定しているため、ブロック6の《9》は《X:7 Y:6》であることがわかります。
数独-難問手順.7-ブロック3に入る《2》を確定させます。
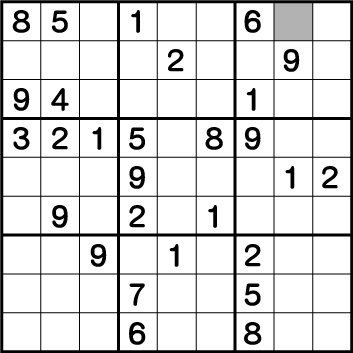
まずは、現在の数字配置で《2》が入る可能性があるマスを洗い出します。
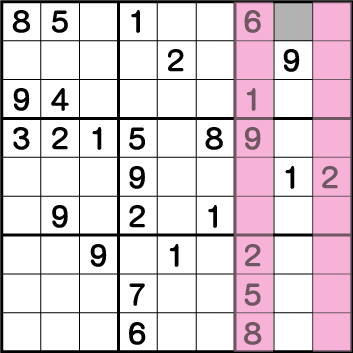 このように、ブロック3に入る《2》の候補は《X:8 Y7/9》の2マスに絞ることができました。次に行で《5もしくは8》のみしか入れることができない専用マスを洗いだします。
このように、ブロック3に入る《2》の候補は《X:8 Y7/9》の2マスに絞ることができました。次に行で《5もしくは8》のみしか入れることができない専用マスを洗いだします。
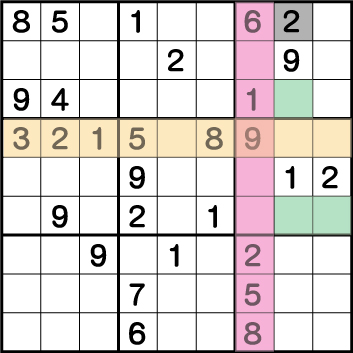 まず、ブロック5に入ってる《5と8》の行から、ブロック6にはグリーン部分の《X:8/9 Y:4》に《5もしくは8》が入ることが確定しています。さらに、ブロック9にはすでに《5と8》が使用されていて、ブロック3の《Y:9》の行ではすでに《5と8》が使用されています。
まず、ブロック5に入ってる《5と8》の行から、ブロック6にはグリーン部分の《X:8/9 Y:4》に《5もしくは8》が入ることが確定しています。さらに、ブロック9にはすでに《5と8》が使用されていて、ブロック3の《Y:9》の行ではすでに《5と8》が使用されています。
つまり、《X:8》の列を見た時に、《X:8 Y:4/7》の2マスは《5と8》しか入れることができな5・8専用マスであることが確定します。結果、《X:8 Y:7》に《2》を入れることができず、残った《X:8 Y:9》が2であることが確定します。ブロック3の《2》が確定したら・・・
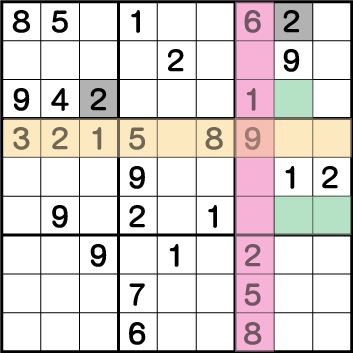 そのままブロック1の《2》も確定します。
そのままブロック1の《2》も確定します。
数独-難問手順.8-ブロック1の《7》を背理法で確定させます。
この問題の一番の難所になってきます。通常テクニックでは前述までで手詰まりとなりますが、ここで背理法を使用してゲームを進めていきます。まずは、《X:3 Y9》に入る数字を洗い出します。
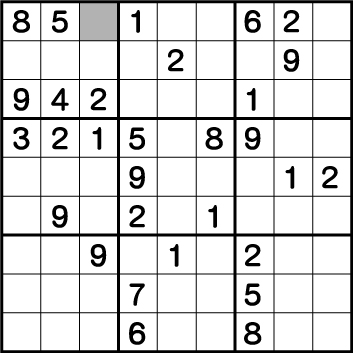 分かりやすいようラインを引くと・・・・
分かりやすいようラインを引くと・・・・
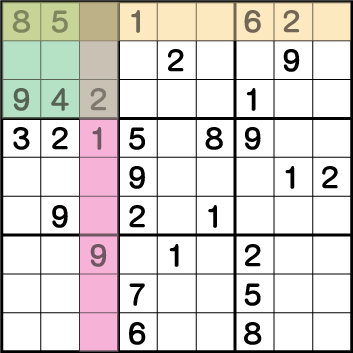 列・行・ブロックで使用されていない《3と7》が候補してあげられます。当然ですが、どちらかが正解でどちらかが不正解となります。「ならば、とりあえずどちらかを入れて見よう。」というのが背理法です。
列・行・ブロックで使用されていない《3と7》が候補してあげられます。当然ですが、どちらかが正解でどちらかが不正解となります。「ならば、とりあえずどちらかを入れて見よう。」というのが背理法です。
ちなみにここに3を入れて数独を進めていくと・・・・
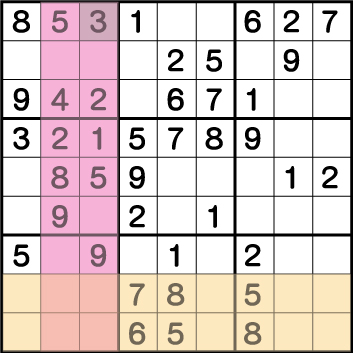 このようになり、見ての通りブロック7に《8》を入れるマスが無くなってしまいました。つまり問題として矛盾がでてしまったので、《X:3 Y:9》は残りの候補の《7》が正解となります。
このようになり、見ての通りブロック7に《8》を入れるマスが無くなってしまいました。つまり問題として矛盾がでてしまったので、《X:3 Y:9》は残りの候補の《7》が正解となります。
数独-難問手順.9-ブロック8の8を確定させます。
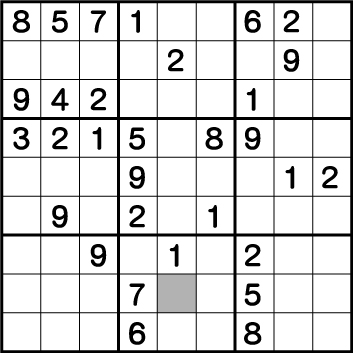
まずは、グレー部分の《X:5 Y:2》に入る候補を洗いだします。
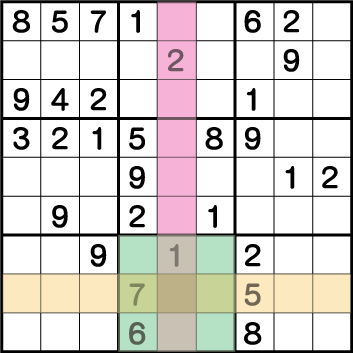 少し候補としては多いですが、列・行・ブロックから、まだ使用されていない数字は《3・4・8・9》ということがわかります。
少し候補としては多いですが、列・行・ブロックから、まだ使用されていない数字は《3・4・8・9》ということがわかります。
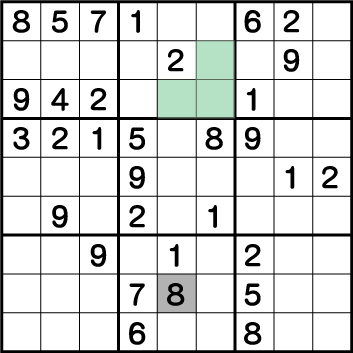 次にブロック2の《X:5 Y:7》そして《X:6 Y7/8》の3マスに入る数字を洗い出します。
次にブロック2の《X:5 Y:7》そして《X:6 Y7/8》の3マスに入る数字を洗い出します。
《X:5 Y:7》の候補は《3・5・6・7・8》
《X:6 Y:7》の候補は《3・5・6・7》
《X:6 Y:8》の候補は《4・5・7》
となります。ここで洗いだした数字の《5・6・7》は他のマスでは絶対に使用することはできません。つまり、グリーン部分のエリアは《5・6・7》のみの専用マスとなり、《X:5 Y:7》では最初に候補としてあげたいた《7と8》を入れることができないことが確定します。すると《X:5》の列で見た時、《8》の候補として残ったのが《X:5 Y:2》となります。
※前述までで、この難問も山場は越えました。ここからは、難易度が急激にさがるので手順を大幅に省略しますが、ここまでの内容が理解できている方なら、すぐにわかるかと思います。
数独-難問手順.10-全てのブロックの《5・8》を確定させます。
前述までで、この難問も山場は越えました。ブロック8の8が確定したら、芋づる式で全てのブロックの《5・8》を確定させることができます。
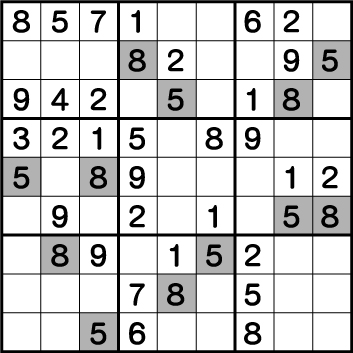
数独-難問手順.11-ブロック2・3・8の(一部の)《3と4》を確定させます。
現在の数字配置で、《X:4 Y:7》に入る候補は《3》しかありません。するとブロック3の《3》、そしてブロック7の《4》を連続で埋めることができます。
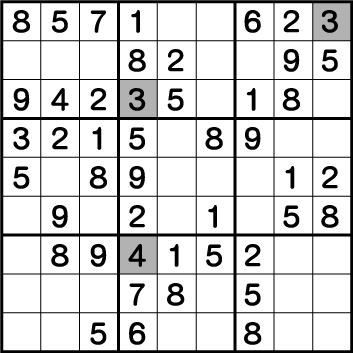
数独-難問手順.12-ブロック3の《7》を基点に各ブロックの《6と7》を確定させていきます。
前述の配置ですでに《X:9 Y:7》の《7》が確定しているので、そこから各ブロックの《6と7》の大部分を埋めることができます。
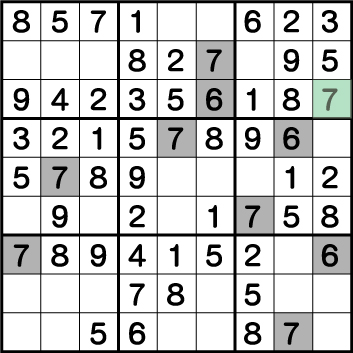
数独-難問手順.13-最終回答
機械的に空きマスを埋めていくだけなので、手順を全て省きます。

まとめ-数独-超難問集1/10-解答
今回の難問のネックは手順.8の背理法ですね。通常のテクニックでどうしても手詰まりになってしまった場合に有効活用できる手法です。
ですが矛盾点が見つかるまでにかなり先まで数独を進める必要が出てくる場合があるため、できる限り使用したくない手ではあります。数独の難問ではおなじみの手法ではあるので、覚えておきましょう。

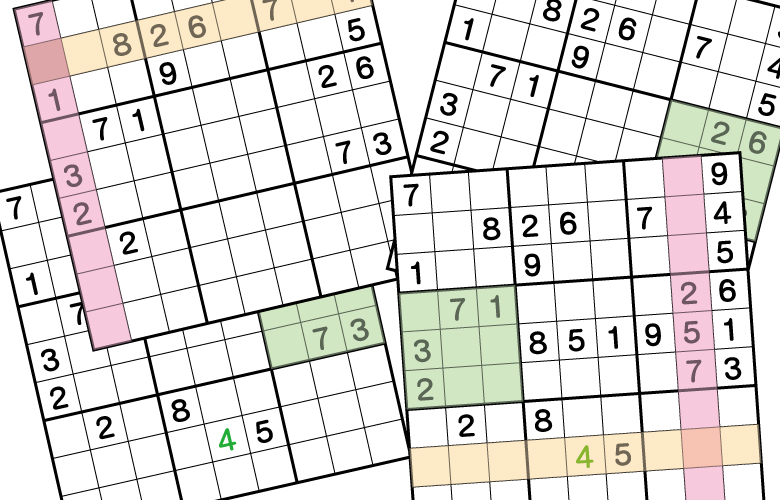





背理法の代案です。
85ー ーーー ーーー
ーーー ー2ー ーーー
ーーー ーhー ーーー
ーーー 5ー8 ーーー
ーーc ーーー ー12
ーーー ーーー ーab
ーー9 f1g ーーー
ーーd ーーー 5ーー
ーーe 6ーー 8ーー
ab58です。
すると deの少なくとも1つに 58どちらかが入ります。
それは fgどちらかに入り さらに hに入ります。
つづいて
ーーー ーーー 6ーー
ーーー ーーー ーーー
942 ーhk 1mn
321 5X8 9ーー
ーーー ーーー o12
ーーー ーーー pab
ーーー ーーー 2ーー
ーーー 7ーー 5ーー
ーーー 6ーー 8ーー
kに6が入り mnどちらかに7が入ります。
それは さらに opどちらかに入り Xに入るので
X7とわかります。