数独の解き方【テクニック一覧】初級から超上級テクニックまで！

数学の問題を解くのに必要な公式（テクニック）がいくつも存在するように、ペンシルパズルゲームの数独にも数多くのテクニックが存在するのをご存じでしょうか？数独を効率よく解いていくためにはこのテクニックが必要不可欠になってきます。

数独を解くための14種類のテクニックを解説

ここでは、数独を解くためのテクニックを《初級-4つ》《中級-2つ》《上級-8つ》に分け全14種紹介していきます。ここで紹介するテクニックを駆使することで、解けない数独が解けるようになったり、時短にも期待できると思いますので参考にしてみてください。

説明を始める前に、わかりやすいように各所の呼び名を決めておきたいと思います。

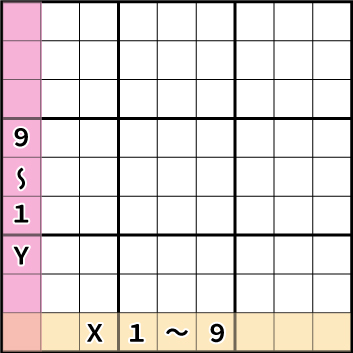
左下を基準に行（横）をX1～9、
そして、列（縦）をY1～9とします。

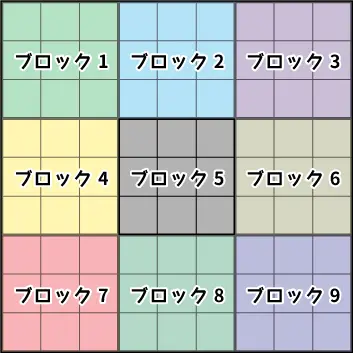
次に左上を基準に3×3マスの9マスをブロック1～9とし説明していきたいと思います。「数独って？」「数独のルールは？」という方は下記の記事を参考にしてみてください。数独の基本ルールを紹介しています。

数独の解き方-初級テクニック編

まずは初級テクニックから。初級テクニックでは、フルハウスやシングルと言った、数独のルールーにまつわる超基本的なテクニックのみの紹介となります。特にシングルは簡単な問題から難問まで共通して何度も使用するテクニックなのでしっかりとマスターしましょう。

解き方その①-フルハウス

【ブロック】や【列】・【行】単位で見た時、すでに8つの数字がマスに埋まっている状態で９つ目の数字を見つけ出す手法となります。数独の基本中の基本です。よほど、難易度の低い数独でない限り序盤で使用することはほとんどありません。

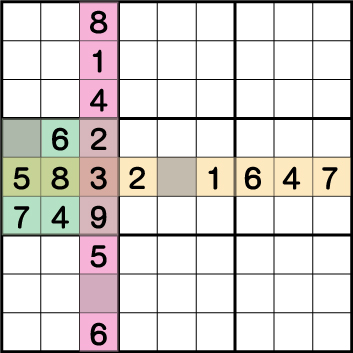
数独は、【ブロック】・【列】・【行】各々、１～９を１度しか使用できないという制約があります。フルハウスは各エリアですでに８つの数字が確定している状態で９つめを見つけ出すテクニックとなります。テクニックといっても、１～９を数えて抜けている数字を入れていくだけの基本中の基本テクニックとなります。

この例では・・・
ブロック《X:1 Y:6》＝【1】
列　　　《X:3 Y:2》＝【7】
行　　　《X:5 Y:5》＝【9】
ということがわかると思います。

解き方その②-隠れたシングル

同数が入る【列】や【行】または、これらの組み合わせから、残ったマス目の数字を確定させるテクニックとなります。隠れたシングルは数独の最初から最後までお世話になる、最も多用するテクニックでもあります。

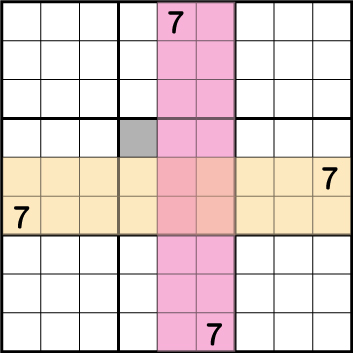
この例の場合、各ブロックに点在する【7】の配置から《X:4 Y:6》＝《7》ということがわかります。

解き方その③-裸のシングル

一つのマスに注目し、そのマスが属する【ブロック・列・行】からまだ使用されていない数字をみつけるテクニックとなります。

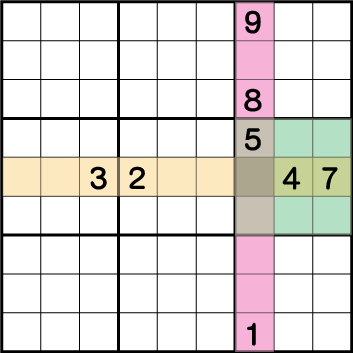
この例では《X:7 Y:5》に注目してみると・・・・
ブロックで《4・5・7》
列で　　　《1・5・8・9》
行で　　　《2・3・4・7》
が使用されていて、まだ使用されていない数字が《6》のみということがわかります。結果《X:7 Y:5》＝《6》ということがわかります。

解き方その④-ロックされた候補

あるマス目Aに入る（予定）の数字の影響を受けて関連するマス目Bから候補となる数字を除外したり、逆に確定させたりするテクニックとなります。

この例で言うと《X:3 Y:5》＝《3》が確定することで、《X:4/5/6 Y:6》のいずれかに《3》が入ることが確定します。逆にこのことで、《X:7/8/9 Y:6》から《3》が候補から除外され、《X:7/8/9 Y:4》のいずれかに《3》が入ることが確定します。このようなテクニックを【ロックされた候補】と呼びます。

数独の解き方-中級テクニック編

中級テクニックになると急に難易度が上昇します。特に三国同盟の4つの形は覚えておかないと見落としがちになるので、注意が必要です。また、隠れ同盟シリーズも見落としがちになります。特定の要素だけでなく、多面的に問題を見ていく力も必要になってきます。

解き方その⑤-二国同盟・三国同盟・四国同盟

Xマスに入る数字がX個に限定される場合、それらが属する【ブロック】や【列】・【行】からそれらの候補を削除するテクニックとなります。

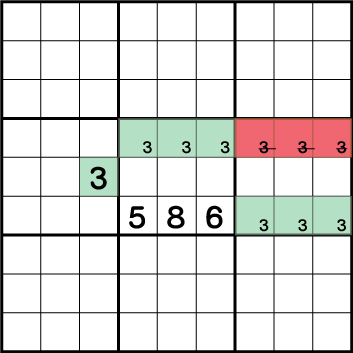
この例では、行《Y:5》の空き2マスがまだ確定することができていません。ただ、確定はしませんがいずれのマスも入る数字の候補は《1もしくは2》ということが確定しています。

つまり、《X:4/6 Y5》＝《1もしくは2》が確定しているため、ブロック5の他のマスからは《1と2》を候補から除外することができるわけです。この考え方が二国同盟となります。

三国同盟の場合も考え方は同じですが少し勝手がことなります。二国同盟の場合は【ブロック・列・行】の同エリアで2つの同数の候補が2か所ある時に成立しました。

もちろん三国同盟の場合も同エリアで3つの同数の候補が3か所ある時に成立するのですが、他にも三国同盟が成立する形が３つあり、合計4つの形が存在します。

上記は全て三国同盟が成立する形となります。特に④番の形は見落としがちになるので注意が必要です。

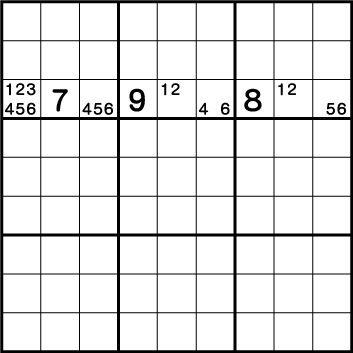
この例では、《1と2》の二国同盟　そして《4/5/6》の三国同盟が成立しています。

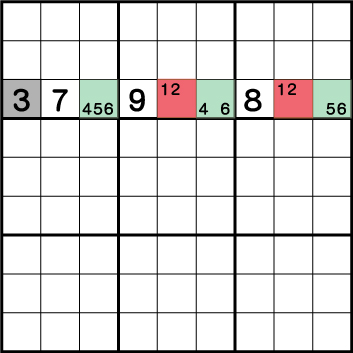
そのため、フルハウスが使用でき、《X:1 Y:7》＝《3》が確定していることがわかります。

解き方その⑥-隠れ二国同盟・隠れ三国同盟・隠れ四国同盟

内容は解き方その⑤と同様ですが、二国（ペア）・三国（トリプル）・四国（クアッド）となる箇所が（隠れていて）１つの要素から特定することができず、特定するためには、複数の要素から絞り込む必要があります。

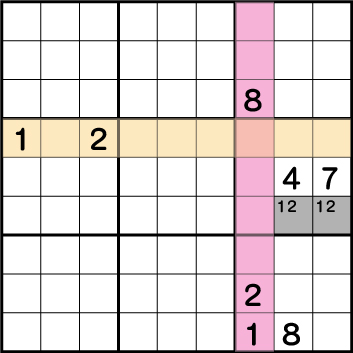
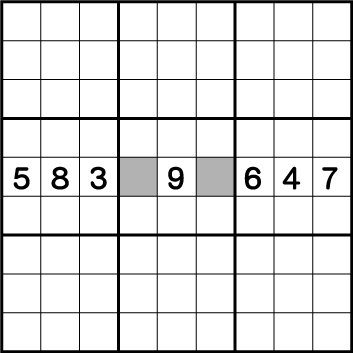
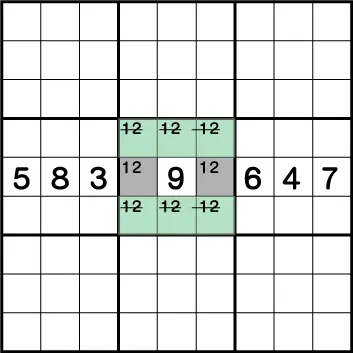
この例では、列《X:7》そして行《Y:6》に《1と2》が使用されています。その為ブロック5で《1と2》が使用できるのは、《X:8/9 Y:4》の2マスのみということがわかります。このように多角的に見ることで見つけることができる同盟を隠れ〇国同盟といいます。

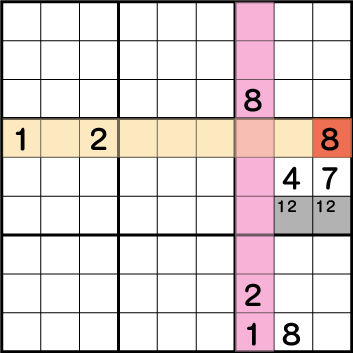
《X:8/9 Y:4》が二国同盟で《1もしくは2》のみの専用マスということがわかれば、《X:9 Y:6》＝《8》ということがわかります。

数独の解き方-上級テクニック編

初級・中級テクニックは、誰かに教えてもらわなくても数独のルールから無意識に使用されている方も多いかと思いますが、上級テクニックになってくると、自然と使用されている方はほとんどおられないと思います。上級テクニックは数独難問には必須テクニックとなるので、初級・中級数独では物足りない方は、是非チェックしてみてください。

解き方その⑦-Xウィング

２つの列（もしくは２つの行）、そしてこれと交差する２つの行（もしくは２つの列）の候補が限定され同じ場合、該当する行（もしくは列）の延長線上からその候補を除外することができるテクニックとなります。

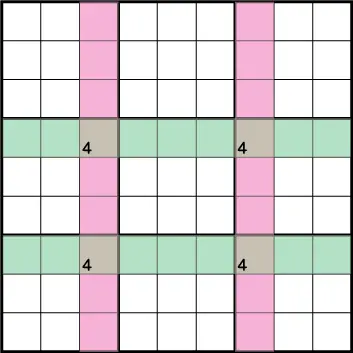
例えば、このように列《X:3》/列《X:7》で見た時に同じ行に候補《4》が入る時、グリーンのエリアから候補《4》を除外することができるテクニックとなります。

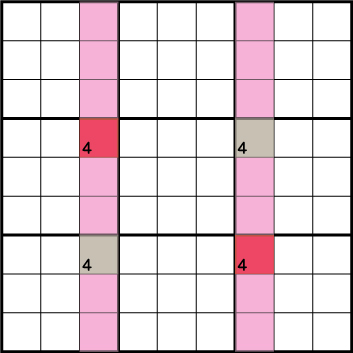
理屈は簡単です。イラストのように井桁状に４か所同数の候補が配列された場合、【赤と赤】もしくは【緑と緑】の2パターンしか存在せず、どちらのパターンになっても候補以外のマスは《4》が除外されることがわかります。

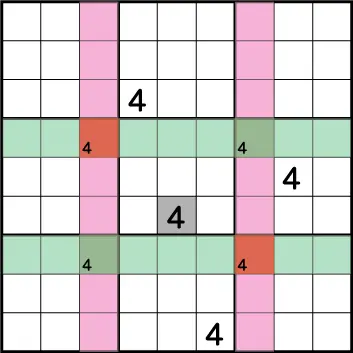
例えばこのような場合、Xウィングを使うことでブロック5に全く数字が入っていない状態でも、《X:5 Y:4》＝《4》とすることが可能になります。

解き方その⑧-スカイスクレイパー

Xウィングの変形で、井桁状態ではなく台形状になっているXウィング。1つの数字で台形型に候補が限定される該当4マスがある時、揃っていない2か所のブロックの一部から候補を除外するテクニックとなります。

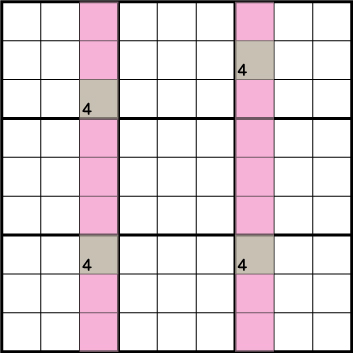
Xウィングの時同様に４が入るパターンを考えて見ます。

《X:3 Y:7》＝《4》の時 《X:7 Y:3》＝《4》、もしくは《X:7 Y:8》＝《4》

《X:3 Y:3》＝《4》の時 《X:7 Y:8》＝《4》 となります。

つまり、どのようなパターンでも必ず、《X:3 Y:7》もしくは《X:7 Y:8》に《4》が入ることになります。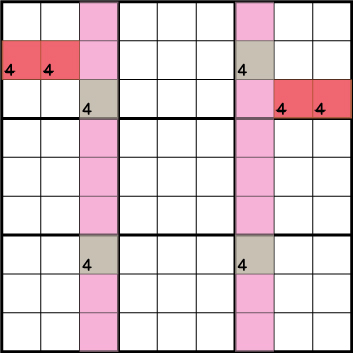

結果このように、《X:3 Y:7》と 《X:7 Y:3》の共通の箇所から《4》を候補から除外することができます。Xウィングを探すときは、一緒にスカイスクレイパーが無いかも確認するようにしておきましょう。

解き方その⑨-ソードフィッシュ

スカイスクレイパー同様にXウィングの発展形となります。３つの列（もしくは３つの行）、そしてこれと交差する３つの行（もしくは３つの列）の候補が限定され同じ場合、該当する行（もしくは列）からその候補を除外することができるテクニックとなります。「Xウィングってなに？」という方は、まず前述で紹介している【解き方その①-Xウィング】から確認してみてください。

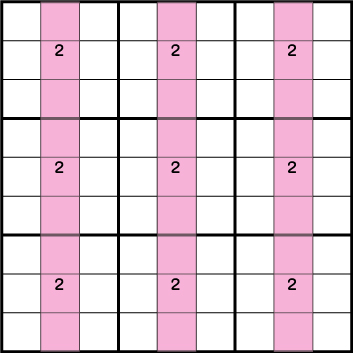
例えば、このように各列に同数の候補が同じ行に配列されている場合にソードフィッシュが使用することができます。

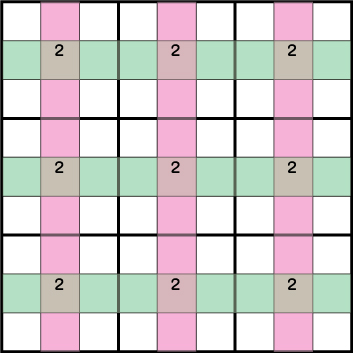
結論を先に言っておくと、このような配置になるのとグリーンエリアから候補《2》を除外することが可能になります。

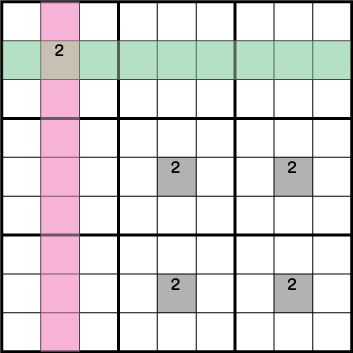
仮に《X:2 Y:8》＝《2》であれば、その他のピンクエリア・グリーンエリアに《2》は入りません。するとグレーのエリアでXウィングの形ができます。

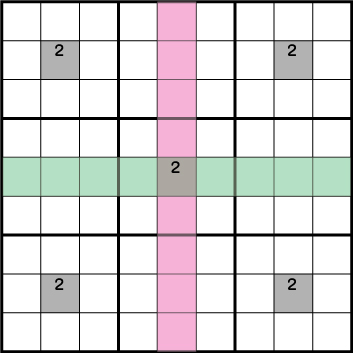
もう一つ例を上げておきます。《X:5 Y:5》＝《2》であれば、その他のピンクエリア・グリーンエリアに《2》は入りません。するとグレーのエリアでXウィングの形ができます。このようにソードフィッシュの形はどこかの数字が確定するとその他の部分で必ずXウィングの形がつくれるわけです。

これらをまとめると、共通するグリーンエリアから候補《2》が除外できることがわかります。

解き方その⑩-XYウィング

三角形のように配置された3つのマスに3つの候補となる数字が《AB》《AC》《BC》のように配置された際に、それらが交差する箇所（とそれに関わる範囲）から特定の数字を候補から除外するテクニックとなります。

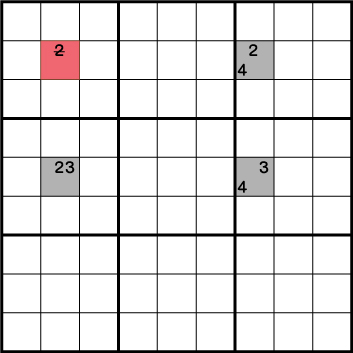
例では、《X:2 Y:8》から《2》が候補から除外されるXYウィングが成立しています。理屈は候補となる数字をマスに入れていただくと簡単に理解できると思います。どのマスにどの候補の数字を入れても必ず《X:2 Y:8》に《2》を入れることができない配置となっています。

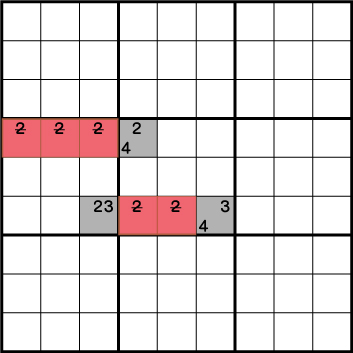
似たような例をもう一つ。マスの配置は違いますが、形は《AB》《AC》《BC》の三角形と同じです。この配置の場合はレッドエリアから候補《2》が除外されます。こちらも全てのパターンで数字を入れていただければ簡単にわかります。どのマスにどの数字を入れても必ずレッドエリアには共通して《2》を入れることができなくなります。

解き方その⑪-XYZウィング

Yウィングの発展形となります。三角形のように配置された3つのマスに3つの候補となる数字が《ABC》《AC》《BC》のように配置された際に、それらが交差する箇所（とそれに関わる範囲）から特定の数字を候補から除外するテクニックとなります。Yウィングより条件が追加されているので、除外候補数もすくなくなります。

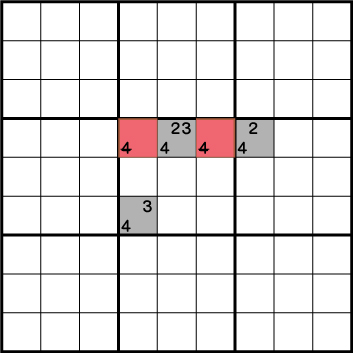
例えばこのような配置の場合、レッドエリアから候補《4》は除外されます。形としてはXYウィングに数字（条件）が一つ追加された状態ですね。《X:5 Y:6》の《2/3/4》を基準に考えた時、3か所のグレーエリアの一つに必ず《4》が入ることがわかります。そしてこれら3つのグレーエリアの共通する箇所がレッドエリアとなります。

解き方その⑫-リモートペア

複数の連なる特定偶数マスが全てABと同じ２種の候補である場合、開始と終点の交差するマスでは候補ABの2種を除外することができるテクニックとなります。出現度がかなり低いテクニックなので、これを必須とする数独はかなりの難問となります。

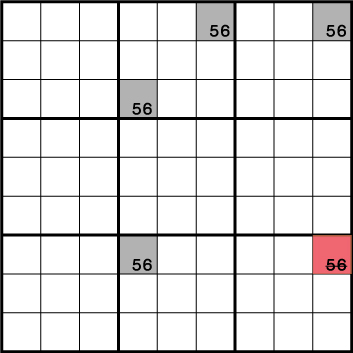
この例ではレッドエリアに候補《5と6》は両方とも候補から除外されることになります。交差に関わる《X:4 Y:3》と《X:9 Y:9》に必ず《5と6》がセットで入ります。そのため、これらが延長線上で交差する《X:9 Y:3》からは《5と6》共に候補課から除外されることになります。

解き方その⑬-XYチェーン

仕組みはリモートペアと似ています。２つの候補で限定された複数マスをチェーンのように辿れ、さらに両端のマスが交差する箇所には、両端に共通する候補を除外できるテクニックとなります。リモートペアは2種の数字で構成されていましたが、XYチェーンは3種以上の数字で構成されています。

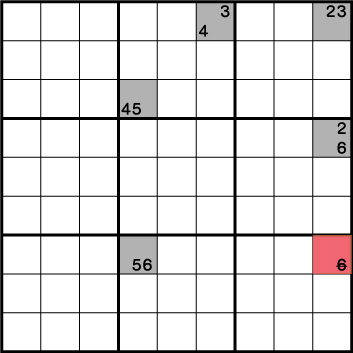
この例ではレッドエリアから、候補《6》を除外することが可能です。レッドエリアに隣接するマスが6であれば当然レッドエリアから《6》が除外さます。

《X:4 Y:3》に《5》を入れた場合は、《X:9 Y:6》＝《6》となります。
そして《X:9 Y:6》に《2》を入れた場合、《X:4 Y:3》＝《6》となります。どちらのパターンであってもチェーンのように周りの数字を辿っていくと、レッドエリアには《6》を入れることが出来ないことがわかります。

解き方その⑭-背理法

数独は数多くのテクニックを駆使して難所をクリアしていくのが醍醐味ですが、どうしても手を進めることができない場合はこの背理法を使用します。背理法は【候補となる数字が少ない（原則２つの）マス】かつ【そのマスが埋まると手が進みそう】な箇所を選択して数独を進めていくテクニックとなります。

誤った数字を選択した場合は手を進めていくうちに矛盾が発生します。その場合、選択した数字は誤りとなり、もう一つの数字が正解となります。逆にたまたま選択した数字が正解であれば矛盾は発生しません。

実際の例は、超難問集の中で何度も使用しているので、下記の記事を参考にしてみてください。

まとめ-数独の解き方【テクニック一覧】

今回は数独の解き方テクニック初級・中級・上級に分けで14種類紹介させていただきました。これらのテクニックを用いればほとんどの数独難問は解くことができるはずです。是非いろいろな数独にチャレンジしてみてください。