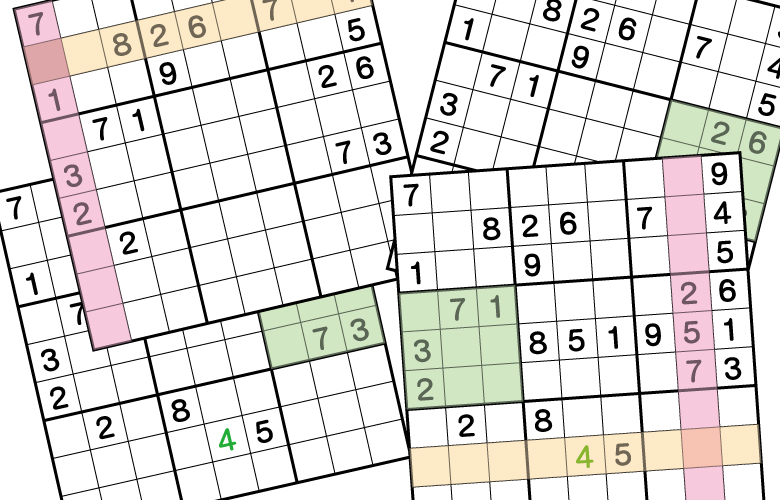
ルールは、《列》《行》《ブロック》に1~9の数字を入れるだけです。ただし、同エリアに同じ数字が入ってはいけません。小学生でもわかる簡単なルールですが、大人でも苦戦するペンシルパズルそれが数独(別名:ナンプレ)です。
ナンプレで遊んで、ギフト券がその場で当たる懸賞に参加しよう。すきま時間にお小遣い稼ぎ。初級から達人級まで豊富な問題。会員登録・メールアドレス不要。
数独で行き詰まったら、確認したい解き方と手順
数独は、ルール自体は単純なので、初級から中級者向けの数独であれば時間をかけるとそのうち必ず解答を導き出すことができますが、要領を得ていないと解答を導き出すまでに相当な時間がかかってしまう場合があります。ここでは、数独の基本的な解き方と、行き詰まった時の解き方を紹介していきたいと思います。
まずは、《数独のルールがわからない人》の為に、数独の基本ルールから確認していきたいと思います。
数独の基本ルール
行き詰まった時の解き方を紹介していく前にまずは、数独の基本的なルールをおさらいしておきたいと思います。ルールは冒頭でお伝えした通り、《列》《行》《ブロック》の各エリアに1~9までの数字がダブらないように入れていくだけです。文章だけだとイメージしづらいのでイラストで確認していきたいと思います。
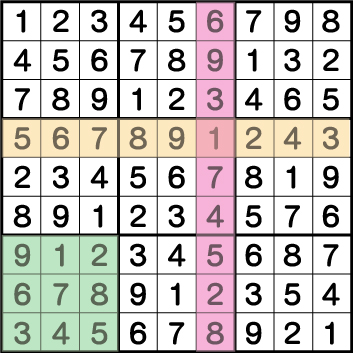
各色の呼び名についてですが、ピンクのエリアが《列》。オレンジのエリアが《行》。そしてグリーンのエリアを《ブロック》と呼びます。各エリア共に1~9の数字がダブリなく入っています。これが数独のルールの全てです。
これから例題をいくつか紹介しながら考えていきますが、ここに紹介している例題(とその応用)で初級から中級難易度のナンプレはほとんど解けるので、早速チェックしていきたいと思います。《確認したい3つの事》は一番下でまとめているので、結論だけを確認したい場合は一番下のまとめまで飛ばしてください。
1.数独の解き方-初級編
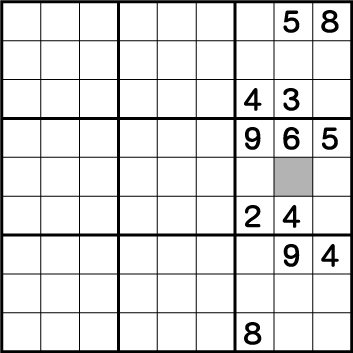
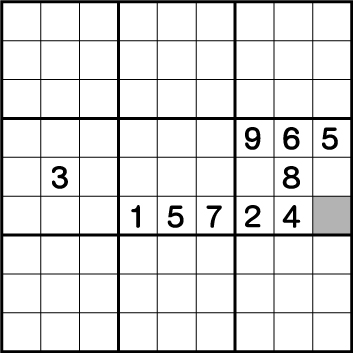
数独は各エリアに同じ数字がダブってはいけなりルールがあるので8に注目します。分かりやすいようにピンクのラインを引きます。
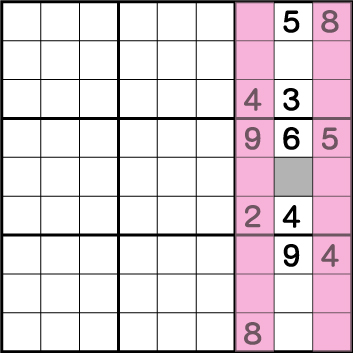
このピンクのライン上には既に8が使用されているので、8を使用することは絶対できません。つまりグレー部分に入れることができる数字は8しかないことがわかると思います。
考え方は同じです。一番の左のブロックの3に注目します。分かりやすいようにこの行にオレンジのラインを引きます。
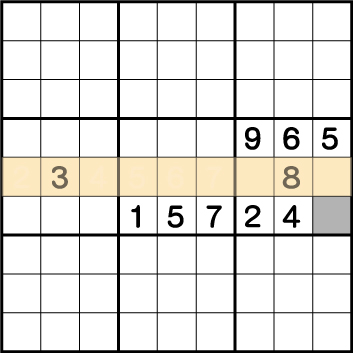
このオレンジのライン上にはすでに3が使用されていて、同ライン上に3を使用することは絶対にできません。つまりグレーに入る数字は3だとわかります。
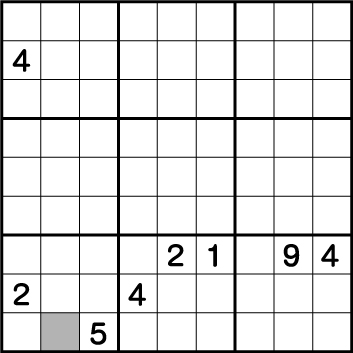
次は、列と行の複合です。数字の多い4に注目します。分かりやすいように4が入っている列と行に色を付けます。
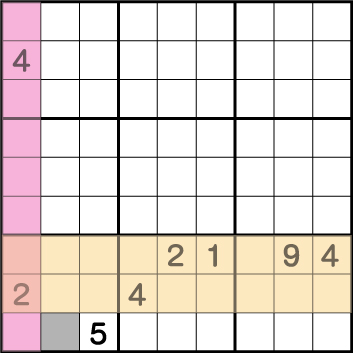
この色のついた部分に複数の4を入れることは絶対にできません。つまり、残り1マス残っているグレー部分が4ということになります。
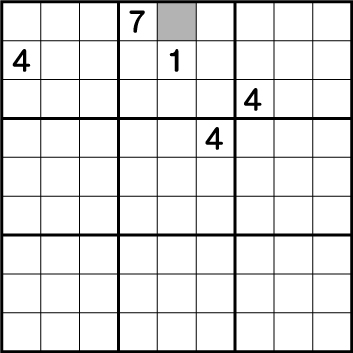
もう一つ似たような行と列の複合問題です。同じく数字の多い4に注目して列と行に色を付けてみます。
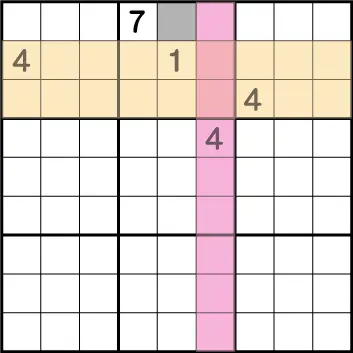
既に4が入っている列や行に再び4を入れることは絶対にできません。つまり残ったグレー部分に4が入ることになります。
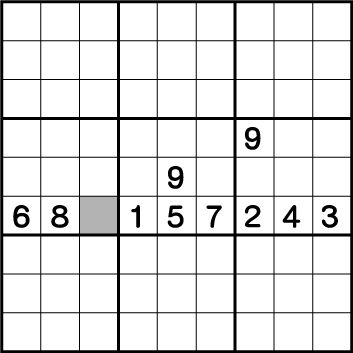
この例では2通りの解き方がありますね。解答を先にいっておくとグレーに入る数字は9ですね。まずは9が入っている行に色をつけてみます。
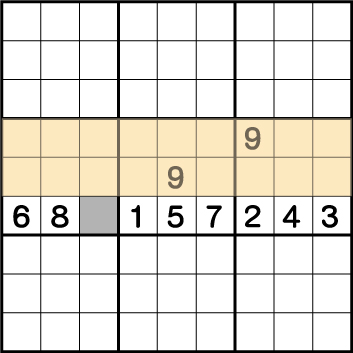
同じライン上に、同じ数字は絶対に使用できないので、空きマスのグレーには9しか入れることができないことがわかります。もう一つの解き方は数字がたくさん入っている一番したの行に注目します。
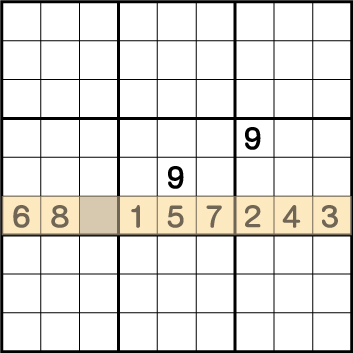
同じ《列》《行》共に同じ数字を2回使用することはできません。行を確認するとすでに、1~8までの数字が使用されています。そのため、グレーに入る数字は9だということがわかります。当然ですが、どちらの解き方でも答えは同じですね。
2.数独の解き方-中級編
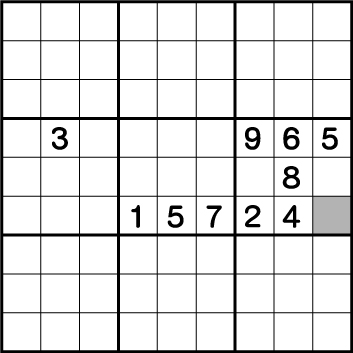
今回は初級編のようにラインを引いても解答は導き出せません。このような場合、ブロックに注目します。わかりやすいようにブロックにグリーンの色を付けます。
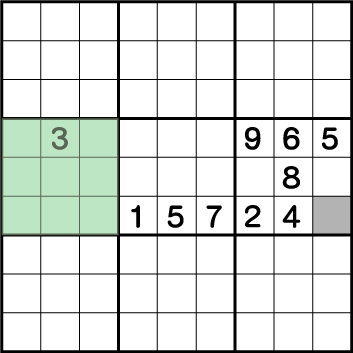
色を付けた部分にはすでに3が使用されているので、同ブロック内に3を入れることは絶対にできません。つまり、他の行が埋まってしまっている該当の箇所には3しか入れることができないことがわかると思います。
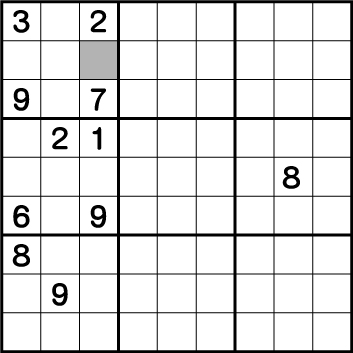
ヒントは不自然に右端のブロックに配置されている8です。ということで今回は8に注目して考えていきます。考え方は、前述と同じで、消去法で考えていきます。数独のルール的に絶対に8をおけない部分に色をつけてみます。
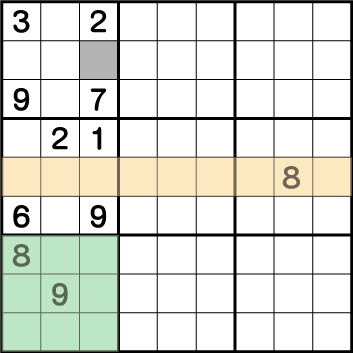
ミドリブロックエリア、そしてオレンジの行はすでに8が使用されているので、同エリアに8を使用することは絶対にできません。つまり列で考えた時、消去法で8が使用できるのは、グレー部分だということがわかります。
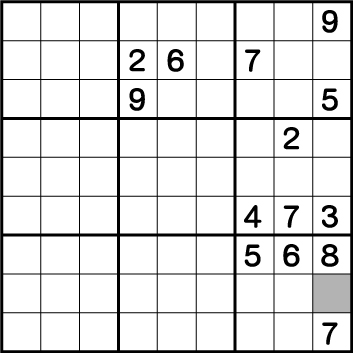
今回は2に注目して考えていきます。まずは既に2が入っていて、2を入れることができない列と行に色を付けてみます。
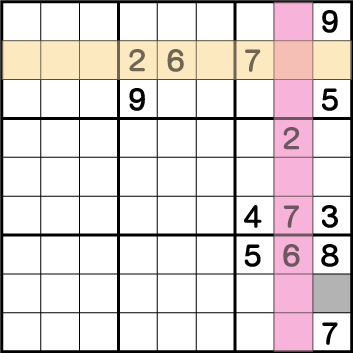
色を付けた列と行には2を入れることができません。ですがこれだけではグレー部分に入れる数字は確定しません。次は右上のブロックに注目します。現状色がついている部分に2を入れることは絶対にできません。つまり2が入るのは7の上下の2か所(グリーン部分)のいずれかになります。
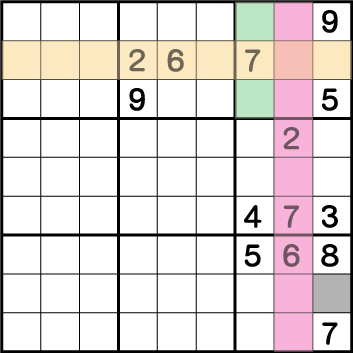
このことから、グリーンの列とピンクの列に2を入れることができません。もちろん2が既に入っている中央ブロックにも2を入れることはできません。つまりグレー部分に2が入るということがわかります。
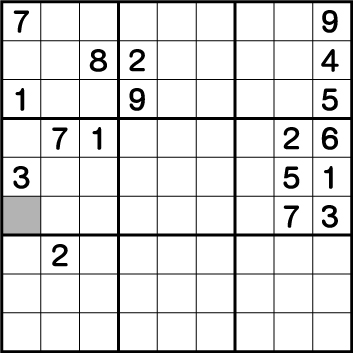
2に注目して考えていきます。まずはすでに2が入っていて使用できないエリアに色をつけてみます。
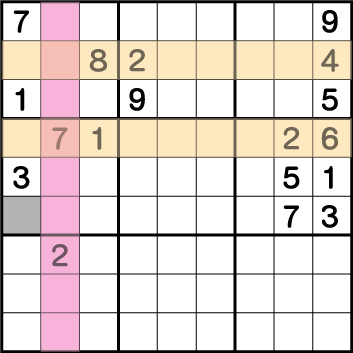
だいぶ絞れてきましたが、まだ入れる数字が確定しません。次は左上のブロックに注目ます。確定はしませんが、グリーン部分のどちらかに2が入ることが確定しており、このグリーンの列には2を入れることはできません。
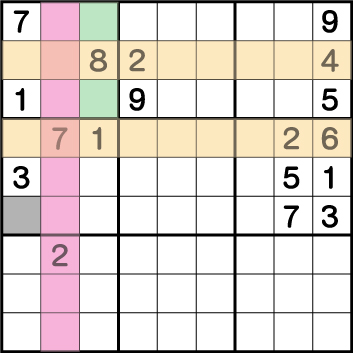
つまり、消去法でグレー部分には2しか入れることができないということがわかります。
3.数独の解き方-上級編
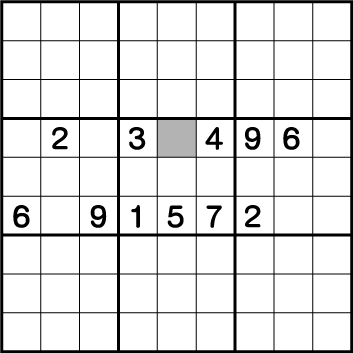
一見するとまだまだ解くのに材料がそろっていないように見えますが、そうではありません。まずは両サイドのブロックと行に注目します。
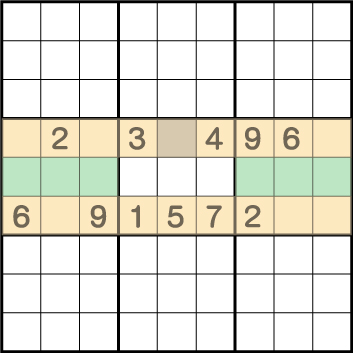
まず、オレンジの行ですでに2.6.9が使用されているので、同じ行で同数を使用することはできません。さらにグリーンは2.6.9が使用さされているブロックなので、同じく2.6.9を使用することはできません。
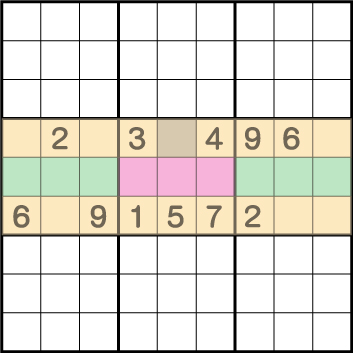
つまり、ピンク部分の各場所の数字は確定しませんが、必ずピンクエリアに2.6.9が入ることが確定します。すると、中央ブロックでは、1.2.3.4.5.6.7.9の数字が入ることが確定するため、残りのグレー部分には8が入ることが分かります。
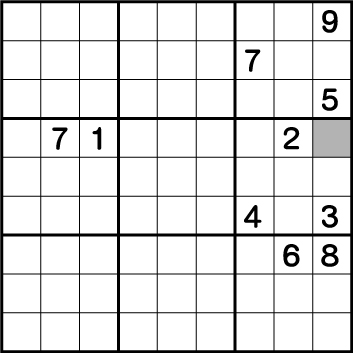
終盤でかなり役立つ方法ですが、なかなか気づきにくい方法です。今回は《列》《行》《ブロック》全てを活用し、消去法で答えを導き出します。
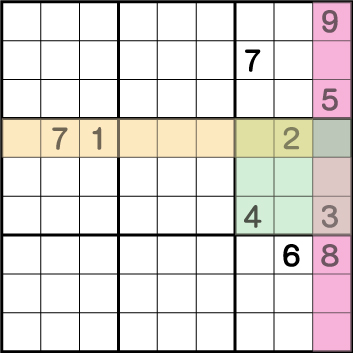
数独は同じエリアに絶対に同数を入れることはできません。つまり・・・ 行で《7.1.2》そして、列で《9.5.3.8》、ブロックで《2.3.4》が使用されています。つまり3つのエリアで使用されていない数字は6のみとなるので、グレー部分には6が入ることがわかります。
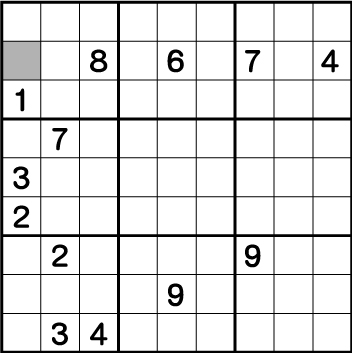
まずは、縦の《列》と横《行》から該当箇所に使用できる数字の候補を探します。
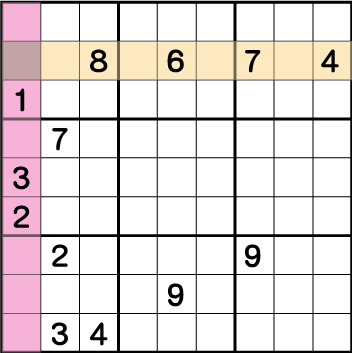
《行》では《8・6・7・4》が、そして《列》では、《1・3・2》が既に使用されています。ここから、グレー部分に入れることができる数字が《5》もしくは《9》であることが分かります。
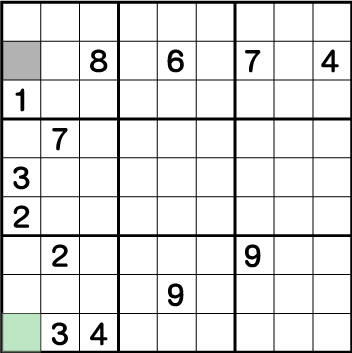
次にグリーン部分に注目するとこの位置には《9》が入ることが確定しているので、グレー部分に入る候補として《9》が消えます。結果残った候補である《5》がグレー部分に入ることが確定します。
番外編-数独の超高難易度のエビル級にチャレンジ
初級~中級問題の数独であれば、前述までで紹介した【行き詰まったら確認した3つの事】をマスターしていれば問題ありませんが、それ以上の難易度になってくると、さらなる上級テクニックが必要になってきます。
ということで、高難易度の数独問題が解けない人のためにエビル(邪悪)級の超高難易度の数独を実践しながら解説していきたいと思います。
超高難易度のエビル級の解説を見る前に・・・
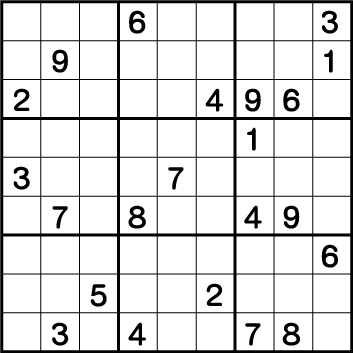
まずは解説見る前に是非ノーヒントで数独エビル級難問にチャレンジしてみてください。
問題は下記リンクから、PDFをダウンロード・印刷することが可能です。
PDF-数独-エビル級問題ダウンロード・印刷
アナログではなくデジタルでチャレンジしたい方は、少し手間ですが、下記のリンク先にて問題を入力することで、デジタルにて数独難問にチャレンジすることが可能です。数独を楽しむことはもちろん、簡単な手順も解析もしてくれるので、参考にしてみても良いかと思います。※背理法等のトライアンドエラーで進める手順は解析されません。
ナンプレを解析。基本戦術で進めることができるナンプレの手順を解説。
解説を始める前に、わかりやすいように各所の呼び名を決めておきたいと思います。
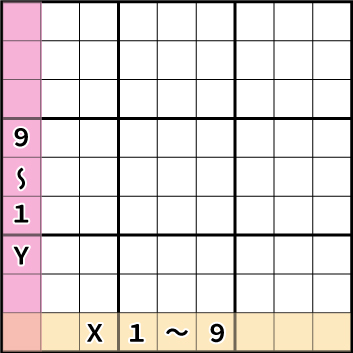
左下を基準に行(横)をX1~9、 そして、列(縦)をY1~9とします。
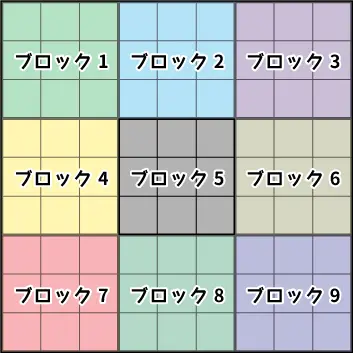
次に左上を基準に3×3マスの9マスをブロック1~9とし説明していきたいと思います。
では、さっそくエビル級超難問数独の解説に入っていきたいと思います。
数独-エビル級問題手順.1-ブロック9の《4》と《9》を確定させます。
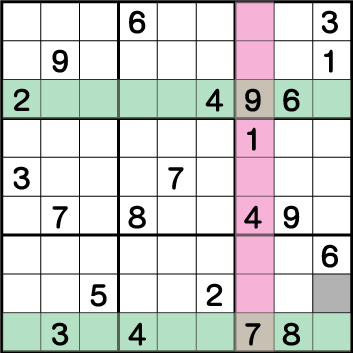
まずは、ブロック2・6・7で《4》を入れることができない列と行わかりやすくラインを引いています。
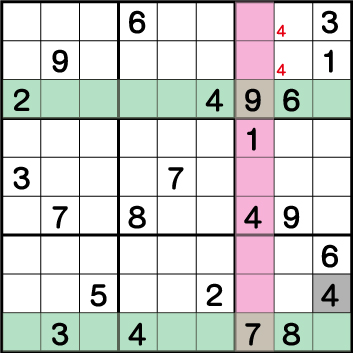
結果、ブロック3には必ず、《X:8 Y:8/9》のいずれかに《4》が入ることが確定します。そのため、ブロック9の《X:8 Y2/3》に《4》を入れることができず、残った《X:9 Y:2》=《4》ということがわかります。
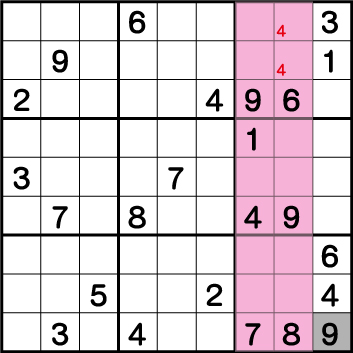
続いて、ブロック9の《4》が確定したら、ブロック3・6の《9》の配置から、ブロック9の《9》が確定します。
数独-エビル級問題手順.2-ブロック6の《6・3》を確定させます。
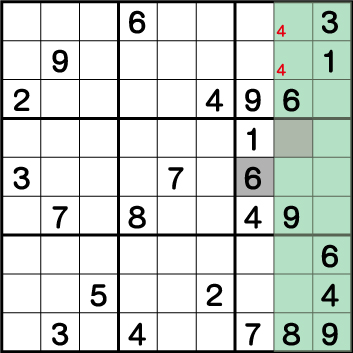
ブロック3、そしてブロック9の《6》の配置から《X:3 Y:5》=《6》ということがわかります。
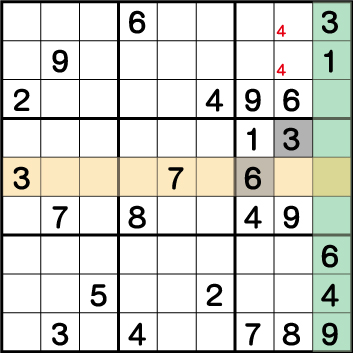
次にブロック3とブロック4の《3》の配置から、ブロック6の《X:8 Y:6》=《3》ということがわかります。
数独-エビル級問題手順.3-ブロック6の《7》を確定させます。
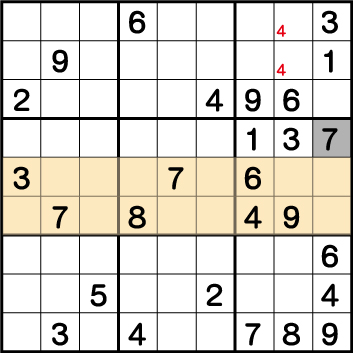
ブロック4、そしてブロック5の《7》の配置から、《X:9 Y:6》=《7》ということがわかります。
数独-エビル級問題手順.4-ブロック5の《4》を確定させます。
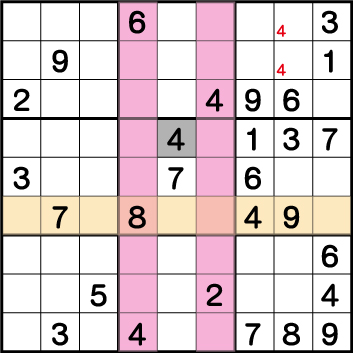
ブロック2・6・8の配置から《X:5 Y:6》=《4》ということがわかります。
数独-エビル級問題手順.5-ブロック7の《2》を確定させます。
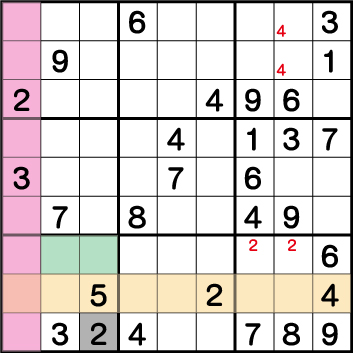
ブロック8の《2》の配置から、《X:7/8 Y:3》のいずれかに《2》が入ることが確定するので、《X:2/3 Y:3》に《2》を入れることはできません。結果《X:3 Y:1》=《2》ということがわかります。
数独-エビル級問題手順.6-ブロック9の《3》と《1》を確定させます。
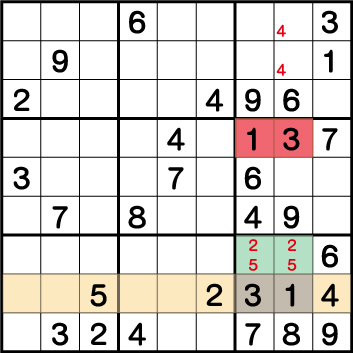
まずは、ブロック7の《5》そしてブロック8の《2》の配置から、《X:7/8 Y:3》=《2/5》ということがわかります。これは、《X:7/8 Y:3》に《2もしくは5》が入る可能性があるという意味ではなく、《X:7/8 Y:3》には、必ず《2と5》が入るという意味となります。このテクニックを二国同盟と言います。
すると、ブロック9の空きマスである《X:7/8 Y:2》=《1/3》ということがわかり、ブロック6の《1/3》の配置から、《X:7 Y:2》=《3》・《X:8 Y:2》=《1》ということが分かります。
数独-エビル級問題手順.7-ブロック9の《2》と《5》を確定させます。
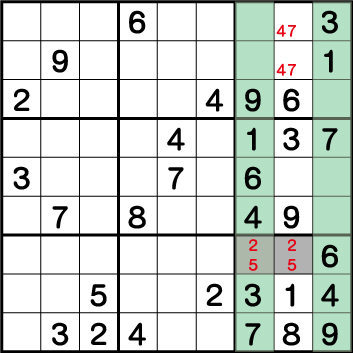
ブロック6・ブロック9のそれぞれの《4》と《7》の配置からブロック3の《X:8 Y:8/9》=《4/7》の二国同盟が成立していることがわかります。つまりこの二つのマスには必ず《4》と《7》が入ることが確定しています。
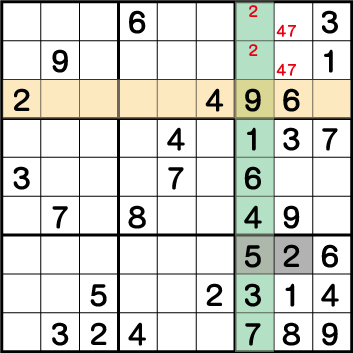
次にブロック1の《2》に注目すると、前述の結果からブロック3に入る《2》は《X:7 Y:8/9》のいずれかであることがわかるため、《X:8 Y:3》=《2》そして《X:7 Y:3》=《5》でであることがわかります。
数独-エビル級問題手順.8-ブロック3・ブロック6の《5》を確定させます。
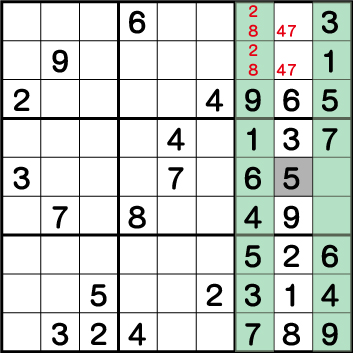
列《X:7》に注目してみると、使用されていない数字は《2》と《8》の二つということがわかります。つまり《X:7 Y:8/9》=《2/8》の二国同盟が成立しています。すぐ隣は《4/7》の二国同盟が成立しています。
つまり、ブロック3で確定していない数字は《5》のみということになります。結果《X:9 Y:7》=《5》ということがわかります。
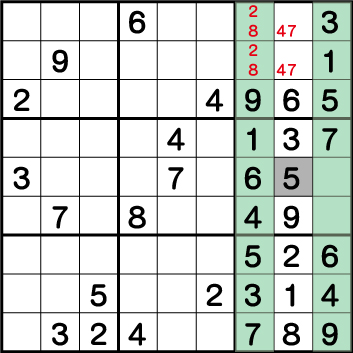
続いて、ブロック3とブロック+9の《5》に注目すると、《X:8 Y:5》=《5》ということがわかります。
数独-エビル級問題手順9-ブロック6の《8》と《2》を確定させます。
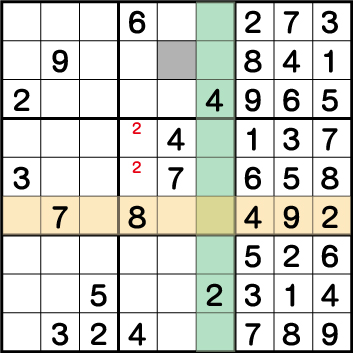
ブロック5の《8》に注目すると、《X:9 Y:5》=《8》ということがわかり、ブロック6の最後の1マスには《2》が入ることがわかります。
数独-エビル級問題手順.10-解けない人続出の背理法
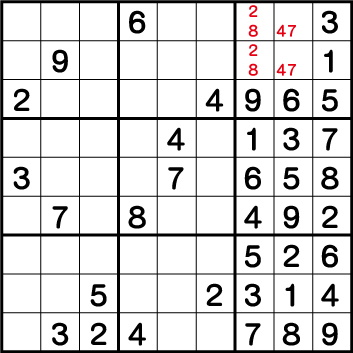
数独中級者程度の方であれば、手順.9までは問題なく解けると思いますが、多くの方が手順10で行き詰まるかと思います。ここは上級テクニックの一つである背理法を使用していきます。
この方法は数字が(少ない候補で)限定されているマスに数字を仮置きをして矛盾点が無いかどうかをチェックするトライアンドエラー方式のテクニックで、数独のテクニックの中で解答をだすのに最も時間がかかることが多い手法となります。
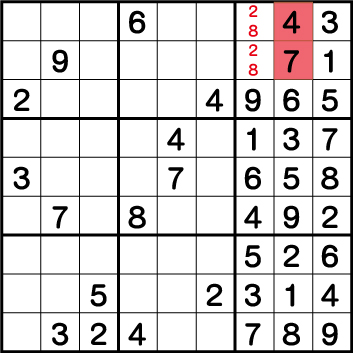
今回は二国同盟がが2つ成立しているブロック3で背理法をためしていきます。とりあえず《X:8 Y:9》に《4》そして、《X:8 Y:8》に《7》を仮置きして矛盾点が無いかどうかを探っていきます。
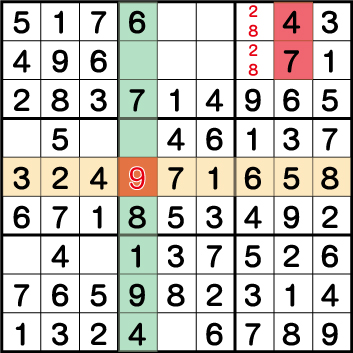
この仮置きのまま手を進めていくと、このようになりました。
行《Y:5》を見た時、《X:4 Y:5》=《9》になるわけですが、既に列《X:4》で《9》が使用され矛盾が発生しています。また、ブロック8の最後の空きマスは《5》を入れたいところですが、同列ですでに《5》は使用されておりここにも矛盾が生じています。
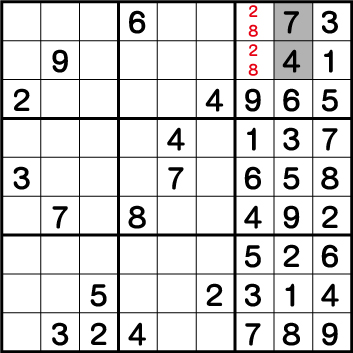
つまり先程、《X:8 Y:9》に《4》そして、《X:8 Y:8》に《7》の仮置きは誤りとなとなるため、《X:8 Y:9》=《7》そして《X:8 Y:8》=《4》が正解となります。
数独-エビル級問題手順.11-解けない人続出の背理法2
通常一つの問題で背理法が複数回必要な問題は少ないですがエビル級の難問は別です。再び、通常手では手が勧められないので背理法を活用していきます。
繰り返しになりますが背理法は原則候補となる数字が少ないところで使用していきます。トライアンドエラーになるので、候補となる数字が多ければ多いほど答えを導き出すのに時間がかかってしまうので、基本的には候補となる数字が2つに絞られている場所で背理法を使用していきましょう。
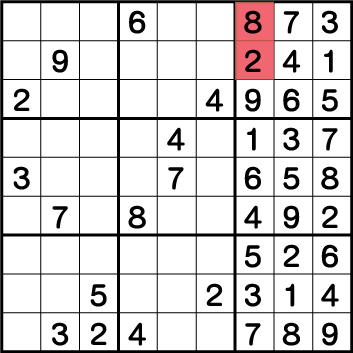
ということで、二国同盟が成立しているブロック3の《2/8》で背理法を行います。
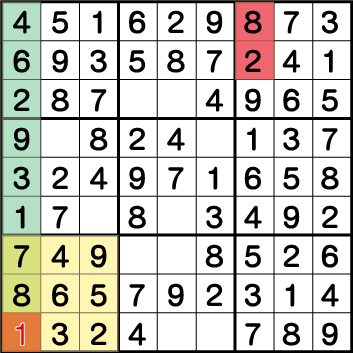
手を進めていくとこのような結果になりました。ブロック7には《1》を入れたいのですが、列《X:1》ですでに《1》が使用されており矛盾が発生しました。
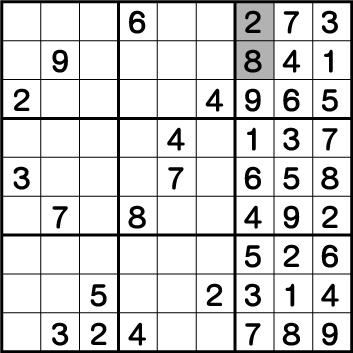
つまり、《X:7 Y:8》が《2》、そして《X:7 Y:9》が《8》は誤りで、《X:7 Y:8》=《8》 《X:7 Y:9》=《2》が正解ということになります。
数独-エビル級問題手順.12-ブロック2の《2》を確定させます。
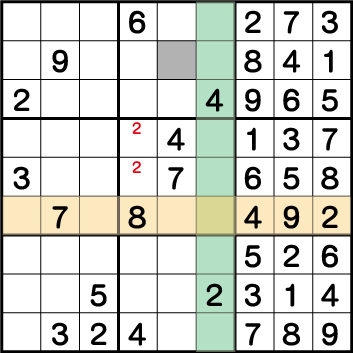
ブロック6の《2》、そしてブロック8の《2》の配置から《X:4 Y:5/6》のいずれかに《2》が入ることが確定します。
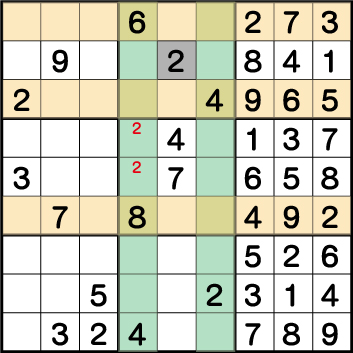
このことを踏まえて《2》を入れることができない箇所にラインを引いてみると、《X:5 Y:8》=《2》ということがわかります。
数独-エビル級問題手順.13-解けない人続出の背理法3
またまた手を進めることができないので、背理法を使用していきます。まずは背理法を使用しやすいマスを探していきます。
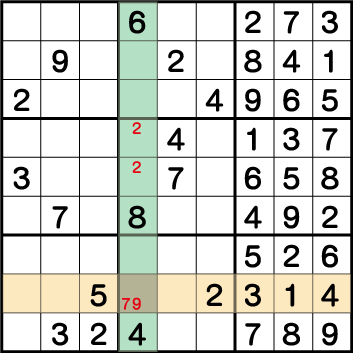
ブロック8の《X:4 Y:2》に注目してみると、列で《1/2/3/4/5》、そして行で《2/4/6/8》がすでに使用されてるため、《X:4 Y:2》=《7 OR 9》であることがわかるので、とりあえず確定していない《7》を仮置きしてゲームを進めて見ます。
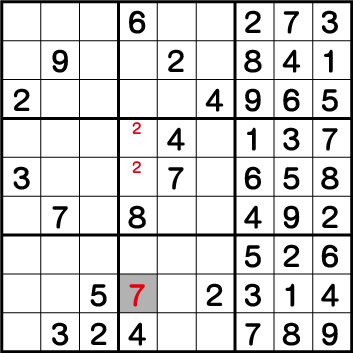
数独-エビル級問題手順.14-ブロック2⇒ブロック1⇒ブロック7の《7》を確定させます。
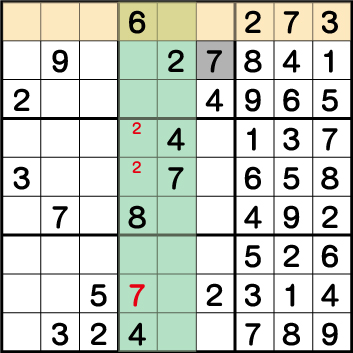
ブロック3・5・8、それぞれの《7》の配置から《X:6 Y:8》=《7》ということがわかります。
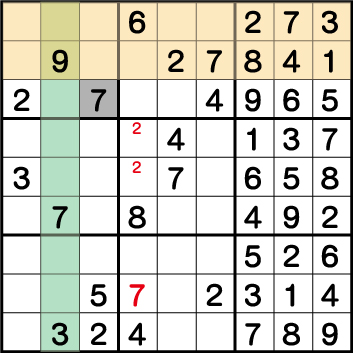
続いて、ブロック2・3・4、それぞれの《7》の配置から《X:3 Y:7》=《7》ということがわかります。
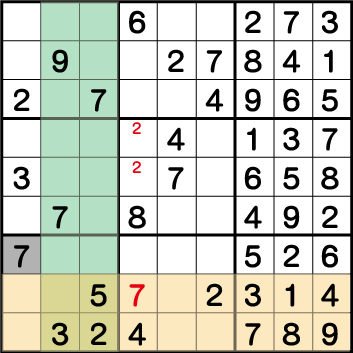
さらにブロック1・4・8・9の《7》の配置から《X:1 Y:3》=《7》ということがわかります。これで全てのブロックの《7》を解くことができました。
数独-エビル級問題手順.15-ブロック1の《3》を確定させます。
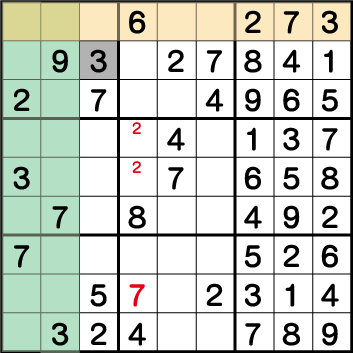
ブロック3・4・7、それぞれの《3》の配置から《X:3 Y:8》=《3》ということがわかります。
数独-エビル級問題手順.16-行《Y:8》の《5》と《6》を確定させます。
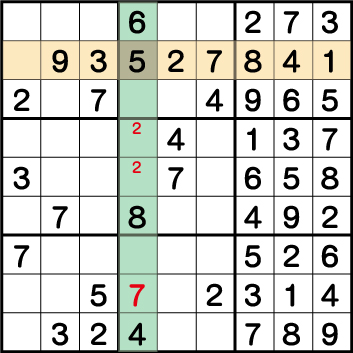
列《X:4》で《4・6・7・8》、行《Y:8》で《1・2・3・4・7・8・9》が使用されています。結果、使用されていない《5》が《X:4 Y:8》に入ることがわかります。
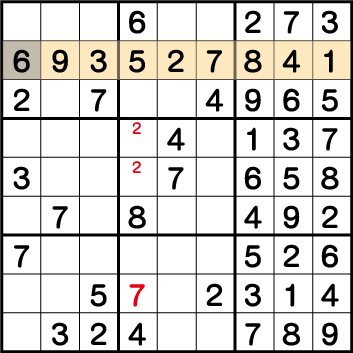
そして行《Y:8》の最後の空きマスは《6》ということがわかります。
数独-エビル級問題手順.17-ブロック7の《6》を確定させます。
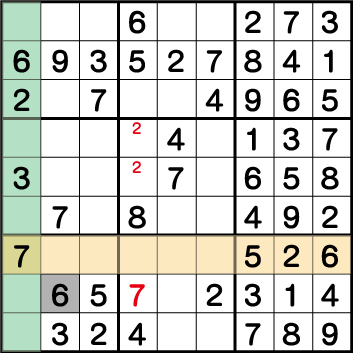
ブロック1の《6》、そしてブロック9の《6》の配置から《X:2 Y:2》=《6》ということがわかります。
数独-エビル級問題手順.18-ブロック7の《1》を確定させます。
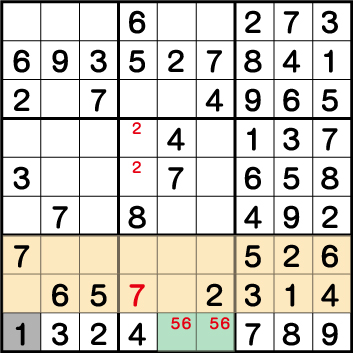
ブロック7、そしてブロック9の《5》と《6》の配置からブロック8で《5》と《6》の二国同盟が成立します。結果、《X:1 Y:1》=《1》であることがわかります。
数独-エビル級問題手順.19-ブロック4の《5》、そしてブロック8の《5》《6》を確定させます。
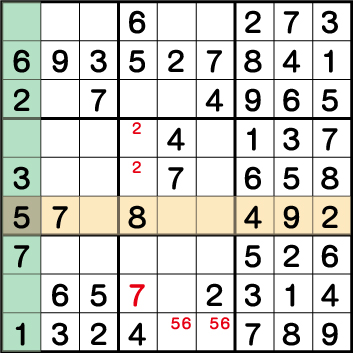
列《X:1》で《1・2・3・6・7》、そして行《Y:4》で《2・4・7・8・9》が使用されています。結果、使用されていない《5》が《X:1 Y:4》に入ることがわかります。
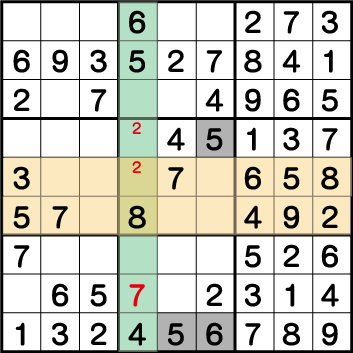
ブロック4の《5》が確定したら、そのままブロック5の《5》が、そしてブロック8の《5》《6》の順に確定させることができます。
数独-エビル級問題手順.20-ブロック1の《4》《5》
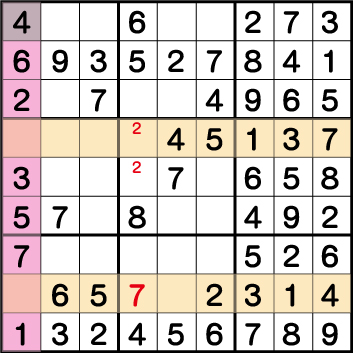
列《X:1》を見た時、行《Y:2/6》ですでに《4》は使用されています。結果《X:1 Y:9》=《4》が確定します。
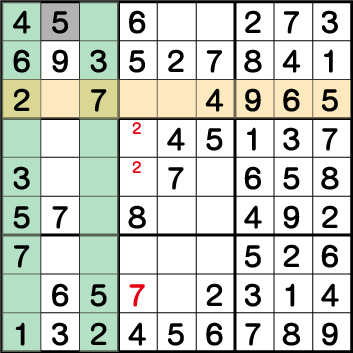
次に、ブロック3・7の《5》の配置から《X:2 Y:9》=《5》ということがわかります。
数独-エビル級問題手順.21-ブロック5の《6》、ブロック4の《6》を確定させます。
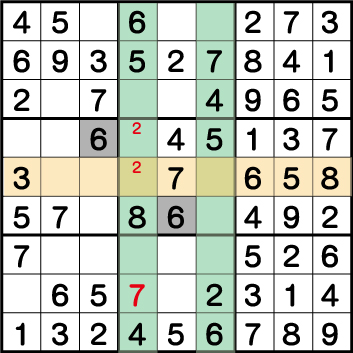
ブロック2・6・8の《6》の配置からブロック5の《6》が確定し、そのままブロック4の《6》を確定させることができます。
数独-エビル級問題手順.22-行《Y:4》の《3》⇒《1》を確定させます。
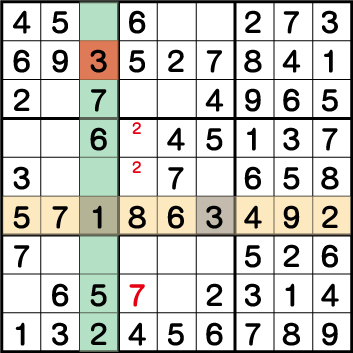
行《Y:4》に注目した時、列《X:3》ですでに《3》が使用されています。結果、《X:6 Y:4》=《3》が確定し、行《Y:4》最後の空きマスには《1》が入ると分かります。
数独-エビル級問題手順.23-ブロック1の《1》そして残りの《8》を全て確定させます。
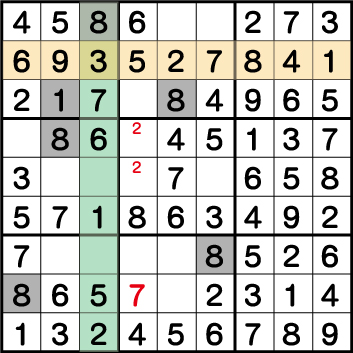
ブロック3の《1》、そしてブロック4の《1》の配置から《X:2 Y:7》=《1》ということが分かります。この《1》が確定すると、同ブロックの《8》が確定し、その後ブロック2⇒ブロック8⇒ブロック4 の順に《8》を確定させることができます。
数独-エビル級問題手順.24-全ブロックの《9》を確定させます。
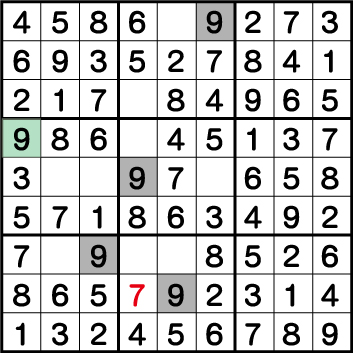
列《X:1》最後の空きマスに《9》を入れ、その後ブロック5⇒ブロック8⇒ブロック2、そしてブロック7の《9》を確定させることができます。
数独-エビル級問題手順.25-残りの空きマスを全て確定させます。

ここまで来ると、後は迷うことなく全てのマスを埋めることができるかと思います。全てのマスを矛盾なく埋めることができたので、手順-13の背理法は《7》で正解ということがわかりました。
仮に《7》で矛盾が出た場合は《X:4 Y:2》=《9》として数独を進めることになります。
まとめ-数独の解き方【行き詰まったら確認したい3つの事】
今回は数独に行き詰まった時の解き方と、超難問エビル級数独についてまとめさせていただきました。最後までもったいぶりましたが、数独に行き詰まったら確認したい3つのことは・・・
1.《列と列》《行と行》《列と行》から限定される数字を探す。
2.《ブロック》を利用した消去法で、導き出せる数字を探す。
3.《列》《行》《ブロック》の消去法で、導き出せる数字を探す。
となります。またこれらを複合して数字を探していく場合もありますが、上記の3つの方法を駆使すれば初級から中級レベルの問題であればほとんど解くことが可能です。
1)は比較的簡単に見つけることができると思います。見つけにくいのは2)と3)となりますが、基本的に数字の多い箇所に注目すると比較的見つけやすいと思います。後は、ポイントとなる箇所を見つけることができるか、できないかだけです。
1)2)3)でいくら考えても行き詰まったままで「マスを埋めることができない・・・」「ナンプレ、わからない・・・」なんて時には、背理法を試してみると良いでしょう。
ちなみに数独には他にも数多くのテクニックが存在します。それらのテクニックは下記の記事でまとめているので良ければ参考にしてみてください。
数学の問題を解くのに必要な公式(テクニック)がいくつも存在するように、ペンシルパズルゲームの数独にも数多くのテクニックが存在するのをご存じでしょうか?数独を効率よく解いていくためにはこのテクニックが必要不可欠になってきま …









1番最後の5が確定するのがわかりません。
グレーのマスの隣はまだ5が入る可能性があるように思えるのですが、その時点でもグレーのマスが確定できるのはどうしてですか?
ご指摘ありがとうございます。問題に誤りがあったので修正させていただきました。
(*- -)(*_ _)ペコリ
グレーのマスのの列と行をみると5と9以外の数字が入既に入っているのでそれら入れることができません。9は一番したに入るのでのこりは5となりす。グレーの横にも5が入りそうですが5以外も入るので5しかはいらないグレーが5になります。
3−2の問題で左下のブロックに2が2つありますよ。
ご指摘ありがとうございます。修正させていただきました。
(*- -)(*_ _)ペコリ
空白の表に自分で入力メモも入れられるそんなアブリはありますか❓
いつも、問題を印刷して挑戦しています。まだ8月分に入っていない状況です。
今回の記事で、頭がスッキリしました。
有難うございます。
今後とも、宜しくご指導ください。
1-2で既に理解出来ない。
何で「3」が入るのが下のライン限定?、上かも知れないでしょう。
下だと断言出来る根拠が乏しい。
どういうことですか?上はもう3つの数字で埋まってますよ?