数独-超難問集4/10-解答

数独-超難問集の4/10問目。変則テクニック必要問題

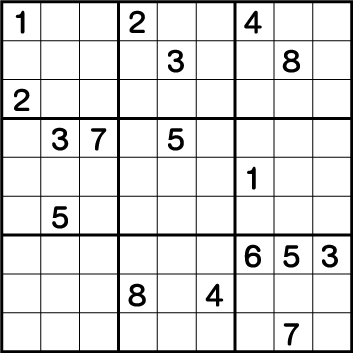
下記の解答を見る前に是非ノーヒントで数独難問にチャレンジしてみてください。
下記のリンクから、PDFをダウンロード・印刷することが可能です。
PDF-数独-超難問集4/10をダウンロード・印刷

アナログではなくデジタルでチャレンジしたい方は、少し手間ですが、下記のリンク先にて問題を入力することでデジタルで数独難問にチャレンジすることが可能です。数独を楽しむことはもちろん、簡単な手順も解析もしてくれるので、参考にしてみても良いかと思います。※背理法等のトライアンドエラーで進める手順は解析されないので注意が必要です。

説明を始める前に、わかりやすいように各所の呼び名を決めておきたいと思います。

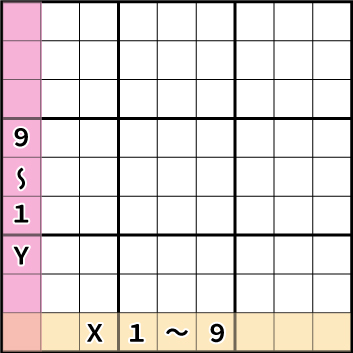左下を基準に行（横）をX1～9、
そして、列（縦）をY1～9とします。

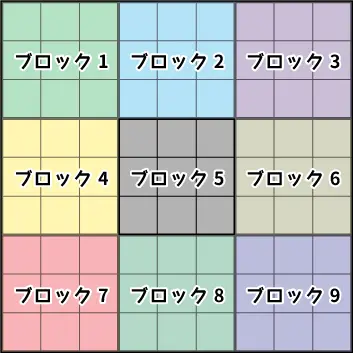次に左上を基準に3×3マスの9マスをブロック1～9とし説明していきたいと思います。ここで紹介している数独は上級者向けの難問となっています。「数独って？」「数独のルールは？」という方は下記の記事を参考にしてみてください。数独の基本ルールを紹介しています。

数独-難問手順.1-ブロック4の《1》を確定させます。

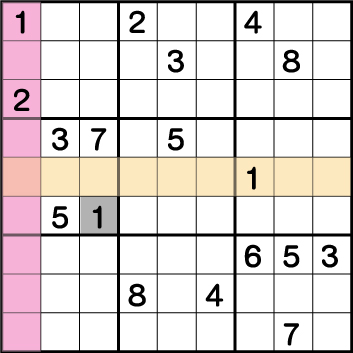ブロック1そしてブロック6の《1》の配置から《X:3 Y:4》の《1》が確定します。

数独-難問手順.2-ブロック7の《3》を確定させます。

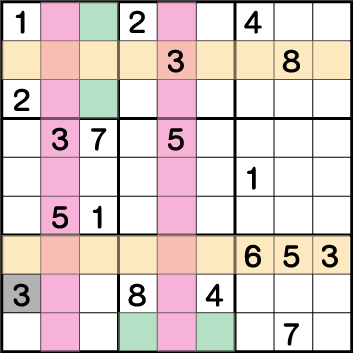基点はブロック2の《3》。
ブロック2、そしてブロック9の《3》の配置で《X:4/6 Y:1》のいずれかに《3》が入ることが確定しているため、《X:1/3 Y:1》から《3》は除外されます。

つぎに、ブロック2そしてブロック4の《3》の配置からブロック1の《X:3 Y:7/9》のいずれかに《3》が入ることが確定しているため、《X:3 Y:1/2》からも《3》が除外されます。結果、《X:1 Y:2》に《3》が入ることが確定します。

数独-難問手順.3-ブロック9の《4》を確定させます。

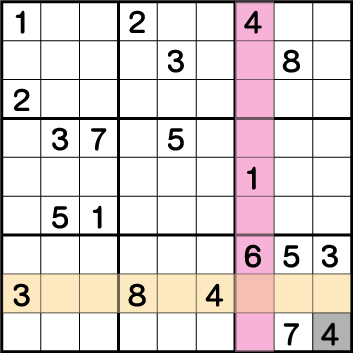ブロック3、そしてブロック7の配置から《X:9 Y:1》が《4》であることが確定します。

数独-難問手順.4-全ブロックの《5》を確定させます。

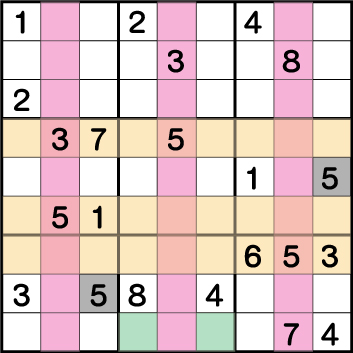まずブロック6についてですが、ブロック9そしてブロック4・5の《5》の配置から《X:9 Y:5》が《5》であることがわかります。次に、ブロック8のグリーン部分《X:4/6 Y:1》のいずれかに《5》が入ることから、《X:1/3 Y:1》から《5》が除外されるため、《X:3 Y:2》が《5》であることが確定します。

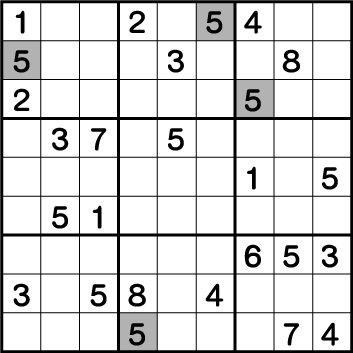あとは、ブロック1　⇒　ブロック3　⇒　ブロック2　⇒　ブロック8　の順に《5》が確定していきます。

数独-難問手順.5-ブロック7、ブロック8の《7》を確定させます。

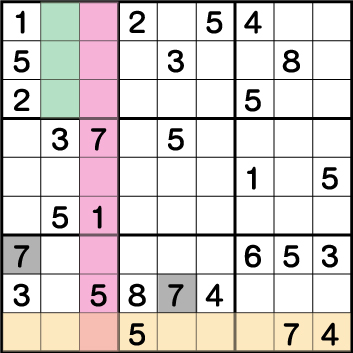まず、ブロック4の《7》の配置から、《X:2 Y:7/8/9》のいずれかに《7》が入ることが確定しているため、同列の《X:2 Y:2/3》から《7》が除外され、結果《X:1 Y:3》に《7》が入ることが確定します。次いで、ブロック8の《7》も確定します。

数独-難問手順.6-ブロック9の《8》を確定させます。

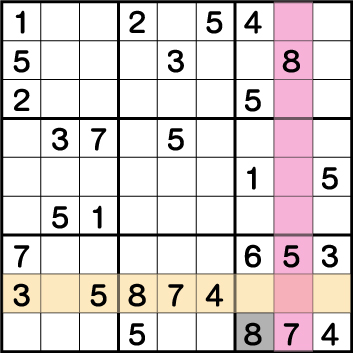ブロック3・ブロック8の《8》の配置から《X:7 Y:1》が《8》であることが確定します。

数独-難問手順.7-ブロック7の《6》を確定させます。

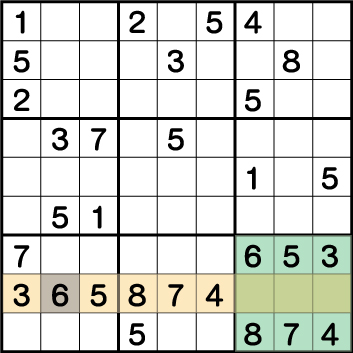ブロック9の中段の3マスは必ず《1・2・9》が入る専用マスとなっています。なので行《Y:2》を見た時、使用されていない《6》が《X:2 Y:2》に入ることになります。

数独-難問手順.8-ブロック5・6・8の《3》を確定させます。

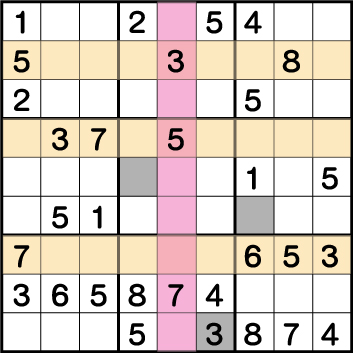まず、ブロック2そしてブロック9の《3》の配置から《X:6 Y:1》の《3》が確定します。次に・・・

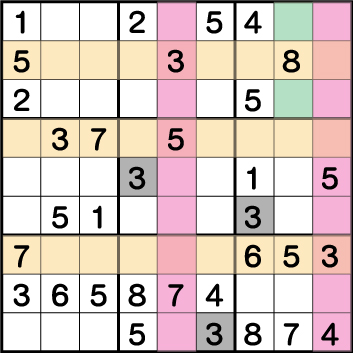ブロック9の《3》の配置からブロック3の《3》はグリーンエリアのみに限定されるため、《X:8 Y4/5》から《3》が除外され、残った《X:7 Y:4》に《3》が入ることが確定します。次いでブロック5の《3》も確定します。

数独-難問手順.9-全ブロックの《7》を確定させます。

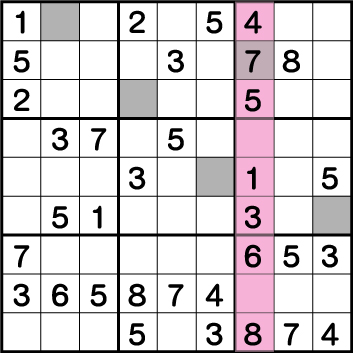まずは、ブロック3の《7》を確定させていきます。列《X:7》の空きマス、全ての候補を洗い出します。すると上から・・・

《X:7 Y:8》＝《2・7》
《X:7 Y:6》＝《2・9》
《X:7 Y:2》＝《2・9》

といことがわかります。このことから《X:7 Y:2/6》は、《2と9》の専用マスということがわかり、《X:7 Y:8》＝《2・7》から《2》が除外され《7》であることが決定します。

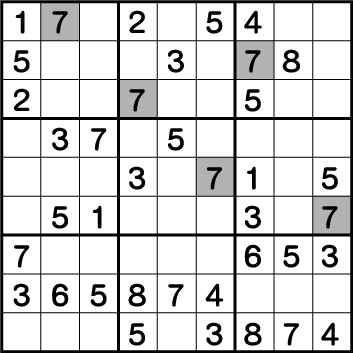ブロック3の《7》が確定したら、ブロック6　⇒　ブロック5　⇒　ブロック2　⇒　ブロック1の順に《7》をマスに入れていくことができます。

数独-難問手順.10-ブロック3の《2》そしてブロック6の《8》を確定させます。

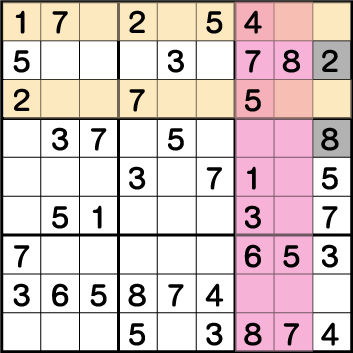ブロック1・ブロック2の《2》の配置から《X:9 Y:8》の《2》が。そしてブロック3・ブロック9の《8》の配置から《X:9 Y:6》の《8》が確定します。

数独-難問手順.11-ブロック8の《6》を確定させます。

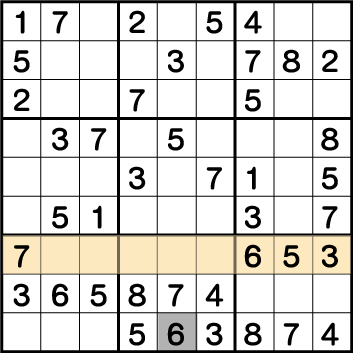ブロック9の《6》の配置から《X:5 Y:1》が《6》と決定します。

数独-難問手順.12-ブロック7の下段3マスの数字を確定させます。

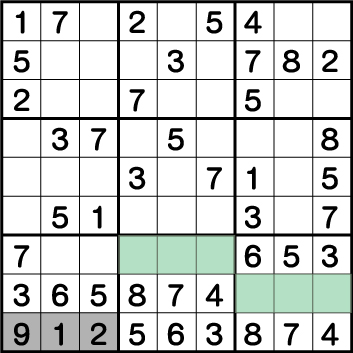まずブロック8、ブロック9の各グリーンエリアはブロックエリアでみることで、それぞれが《1・2・9》の専用マスであることがわかります。このことから、今回埋めていく《X:1/2/3 Y:1》も《1・2・9》の専用マスであることが分かります。

列で見た時《X:1 Y:1》では《1と2》が使用されているため、《9》が確定し、《X:3 Y:1》では同列で《1》が使用されているため、《2》が確定します。残りは《1》しか残っていないので、《X:2 Y:1》では《1》が確定します。

数独-難問手順.13-ブロック4の《2・9》を確定させます。

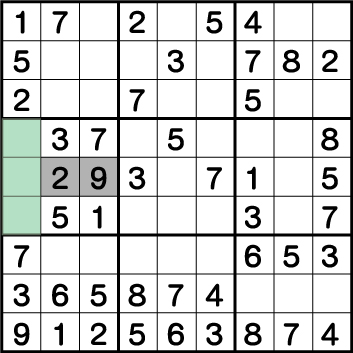ブロック4のグリーンエリアは、列で見ることで《4・6・8》が入る専用マスであることがわかります。つまり《X:2/3 Y:5》の候補としてあげられるのは、《2と9》のみとなります。列で見ることで、《X:2 Y5》に《2》が入ることは容易にわかるので、残りの《X:3 Y:5》に《9》が入ることがわかります。

数独-難問手順.14-ブロック5の《2》を確定させます。

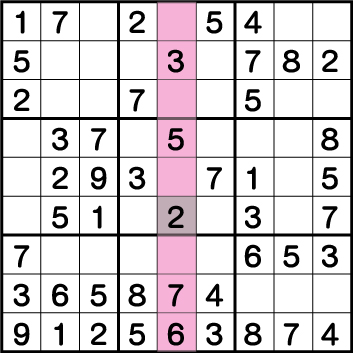
列《X:5》の空きマスに入る候補の数字を全て洗い出します。

《X:5 Y:9》＝《8・9》
《X:5 Y:7》＝《4・8・9》
《X:5 Y:5》＝《4・8》
《X:5 Y:5》＝《2・4・8・9》
《X:5 Y:3》＝《1・2・9》

このことから《X:5 Y:5/7/9》＝《4・8・9》が入る専用マスになっていることがわかるので、他のマスから《4・8・9》を除外します。《X:5 Y:5》＝《2・4・8・9》から《4・8・9》を除外すると《2》のみが残るので、《X:5 Y:4》が《2》とわかります。

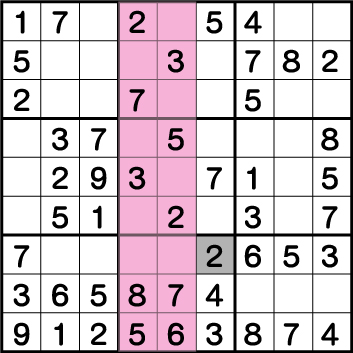ブロック5の《2》がわかると、そのままブロック8の《2》も決定することができます。

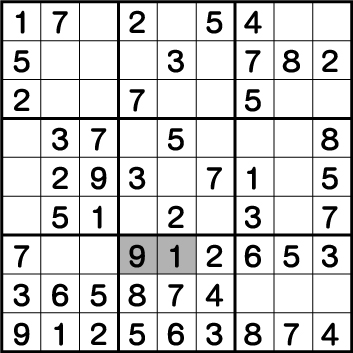さらにブロック8の《2》が確定したことで、《X:5 Y:3》＝《1・2・9》から、前述の《9》そして今回の《2》が除外され《X:5 Y:3》＝《1》となり、最後に残った、《X:4 Y:3》に9が入ることがわかります。

数独-難問手順.15-ブロック1の《9》を確定させます。

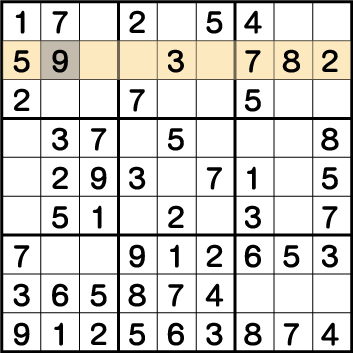行《Y:8》の空き4マスそれぞれに入る数字の全ての候補を洗い出します。

《X:2 Y:8》＝《4・9》
《X:3 Y:8》＝《4・6》
《X:4 Y:8》＝《1・4・6》
《X:6 Y:8》＝《1・6》

このことから、《X:3/4/6 Y:8》は《1・4・6》のみが入る専用マスであることがわかるので、《X:2 Y:8》＝《4・9》から《4》を除外します。結果、《X:2 Y:8》＝《9》となることがわかります。

数独-難問手順.16-ブロック3の《6》を確定させます。

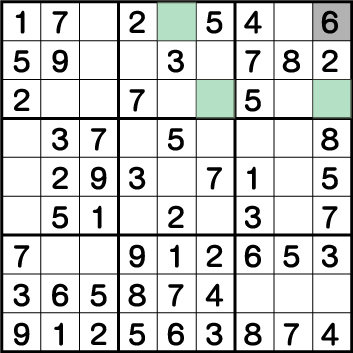
今回の難問数独で最も難しい部分です。もちろん背理法を使用することで手を進めることができますが、今回は背理法を使用しなくても手を進めることができます。

ブロック3は《X:9 Y:7/9》のいずれかに《6》が入ることが確定しています。どちらかに入るかの判別方法についてですが、ブロック2の《X:5 Y:9》を基点に考えていきます。まずは、グリーン3か所、グレー1か所に入る数字の候補を全て洗い出します。

《X:5 Y:9》＝《8・9》
《X:6 Y:7》＝《6・8》
《X:9 Y:9》＝《6・9》
《X:9 Y:7》＝《1・6・9》となっています。

《X:5 Y:9》に《8》を入れた場合、《X:6 Y:7》が《6》となり、《X:9 Y:7》から《6》が除外されます。次に《X:5 Y:9》に《9》を入れた場合、《X:9 Y:9》＝《6》となり、《X:9 Y:7》から《6》が除外されます。つまり《X:5 Y:9》に《8・9》どちらの数字を入れた場合でも結局は、《X:9 Y:7》から《6》が除外されるというわけです。結果、《X:9 Y:9》＝《6》ということがわかります。

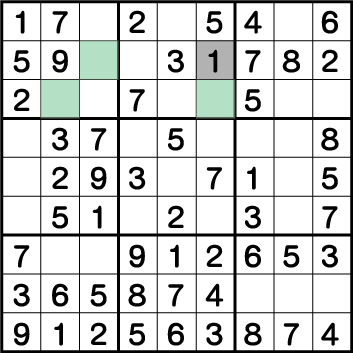
数独-難問手順.17-ブロック2の《1》を確定させます。

求め方は、手順.17と同様です。まずは、該当箇所の候補となる数字を洗い出します。

《X:2 Y:7》＝《4・8》
《X:3 Y:8》＝《4・6》
《X:6 Y:7》＝《6・8》
《X:6 Y:8》＝《1・6》

となります。 《X:2 Y:7》＝《4・8》を基点として考えて見ます。《X:2 Y:7》＝《4》と仮定した時、《X:3 Y:8》＝《6》となり、《X:6 Y:8》＝《1》となります。次に、《X:2 Y:7》＝《8》と仮定した時は、《X:6 Y:7》＝《6》となり、《X:6 Y:8》＝《1》となります。

要は、《X:2 Y:7》に《4・8》のどちらを入れても、《X:6 Y:8》＝《1》にることが確定しています。

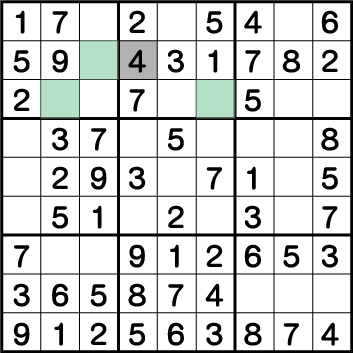
数独-難問手順.18-ブロック2の《4》を確定させます。

求め方は手順16.17と同様です。グリーン・グレー部分に入る数字の候補は・・・

《X:2 Y:7》＝《4・8》
《X:3 Y:8》＝《4・6》
《X:4 Y:8》＝《4・6》
《X:6 Y:7》＝《6・8》となっています。

《X:2 Y:7》＝《4》の時、《X:3 Y:8》＝《6》となり《X:4 Y:8》＝《4》となります。次に、《X:2 Y:7》＝《8》の時、《X:6 Y:7》＝《6》となり、《X:4 Y:8》＝《4》となります。

つまり、《X:2 Y:7》＝《4もしくは8》のいずれかが入っても、 《X:4 Y:8》＝《4》となることがわかります。

数独-難問手順.19-最終回答

手順.18まで終えると、後は機械的に空きマスをうめていくだけです。

まとめ-数独-超難問集4/10-解答

今回、背理法は使用しませんでいたが、手順16～18で変則的な解き方を使用しました。数独といえば、ブロックと行と列というイメージがありますが、数独の難問では今回のように斜めの動きもでてくるので覚えておきましょう。「こういう解き方もある！」と意識していると手詰まりになった時に手が進めやすくなるかと思います。